Градиент функции и его применение

Градиент – характеристика, показывающая направление и величину максимальной скорости изменения функции в данной точке.

Пусть дифференцируемая функция двух переменных.

Градиентом функции называется вектор, координатами которого являются частные производные функции в точке 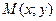и обозначается 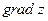, т.е. 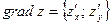или

Теорема 7.1. Градиент функции в точке 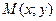характеризует направление максимальной скорости возрастания этой функции в данной точке, причем наибольшая скорость возрастанию функции в точке равна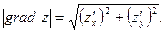

Итак, градиент – вектор, направленный в сторону наибольшего возрастания функции и равный по величине мгновенной скорости возрастания функции.

Пример 7.6. Найти градиент функции .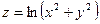

Решение. Вычислим частные производные 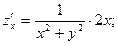Подставив в формулу градиента,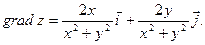

Пример 7. 7. Найти наибольшую скорость возрастания функции 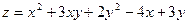в точке .

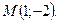Решение. Найдем частные производные и их значения в точке М: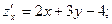

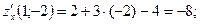
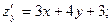
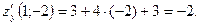
Градиент функции в точке есть вектор 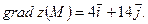Наибольшая скорость возрастания функции равна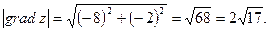

3. Частные производные второго порядка для функции двух переменных

Пусть 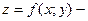дифференцируемая функция двух переменных. Следовательно, для нее можно найти производные 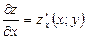и 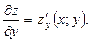Назовем их частными производными первого порядка. В свою очередь они могут быть дифференцируемыми функциями своих переменных и также могут иметь частные производные по каждой их этих переменных.

Частными производными второго порядка от функции называются производные от частных производных первого порядка. Рассмотрим частную производную 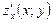. От этой производной возьмем производную по переменной x и по переменной y. Таким образом, 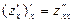и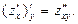

Аналогично получаем 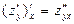и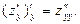

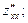
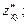
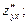
Следовательно, частных производных второго порядка от функциибудет четыре: 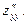Иногда применяют обозначения:

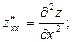
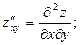
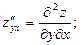
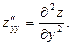
Частные производные 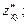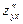называют смешанными производными.

Пример.. Найти частные производные второго порядка функции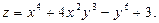

Решение.

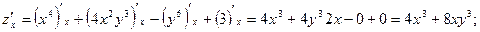
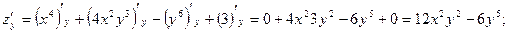
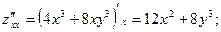
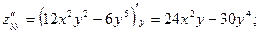
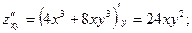
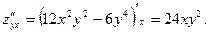
В примере оказалось, чтосмешанные частные производные равны, то есть 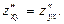Приводимая ниже теорема Шварца (Герман Шварц (1843-1921-немецкий математик), утверждает, что не простое совпадение.

Теорема (Щварца). Если частные производные 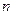порядка непрерывны, то смешанные производные того же порядка, отличающиеся лишь порядком дифференцирования, равны между собой.

В частности, для имеем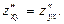

Согласно этой теореме смешанные производные можно вычислять в любом порядке и нет необходимости находить обе смешанные производные.

Частные производные второго порядка используются при нахождении экстремальных значений функции двух переменных.

Дата добавления: 2014-01-20