Экстремум функции двух переменных. Понятие точек экстремума и самого экстремума функции вводится по аналогии с функциями одной переменной

Понятие точек экстремума и самого экстремума функции вводится по аналогии с функциями одной переменной.

Понятие точек экстремума

Точка называется точкой максимума функции , если существует такая окрестность точки 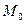, что для всех точек 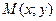из этой окрестности выполняется неравенство

Значение называется максимум функции .

Точка называется точкой минимума функции , если существует такая окрестность точки 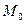, что для всех точек 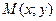из этой окрестности выполняется неравенство

Значение называется минимум функции.

Точки максимума и точки минимума называют точками экстремума. Как и в случае функции одной переменной есть необходимые и достаточные условия существования экстремума.

Теорема (необходимое условие экстремума). Если дифференцируемая функция имеет в точке экстремум, то частные производные первого порядка в этой точке равны нулю, т.е.

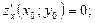
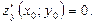
Точки, в которых частные производные первого порядка равны нулю, называются «подозрительными» на экстремум или стационарными.

Если вспомнить понятие градиента функции, то необходимое условие экстремума можно сформулировать так:

Теорема …. Если дифференцируемая функция имеет в точке экстремум, то градиент функции в этой точке есть нулевой вектор.

Замечание 1. Функция может иметь экстремум и в точках, в которых одна или обе производные не существуют, т.е. функция не является дифференцируемой. Например, функция 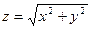имеет минимум в точке 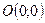, но очевидно не имеет в этой точке частных производных.

Замечание 2. Равенство нулю частных производных первого порядка является лишь необходимым, но не достаточным условием экстремума. Например, для функции 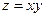частные производные в точке 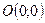равны нулю, но точка 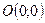не является экстремумом для этой функции.

Теорема (достаточное условие экстремума ). Пусть в стационарной точке и в некоторой ее окрестности функция имеет непрерывные частные производные до второго порядка включительно. Положим

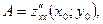
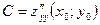
и определим величину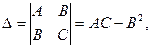

Тогда:

1) если 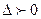, то функция имеет экстремум в точке : максимум при 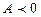и минимум при

2) если 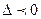, то функция не имеет экстремум в точке ;

3) если 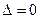, то функция может иметь экстремум в точке , а может не иметь. Требуется дополнительные исследования.

Алгоритм для нахождения экстремумов дифференцируемой функции двух переменных

1. Найти частные производные первого порядка 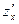и

2. Найти стационарные точки, решив систему

3. Найти частные производные второго порядка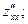

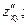
4. Вычислить значения в каждой стационарной точке и для каждой найти значение

5. Сделать вывод о существовании экстремума в каждой стационарной точке на основе достаточного условия экстремума.

6. Найти экстремальные значения функции.

Пример … Исследовать на экстремум функцию

Решение.

1.Найдем и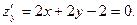

2. Решим систему 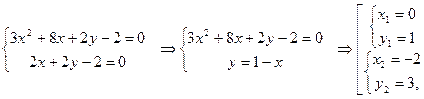Итак, найдены две стационарные точк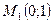и и

3. Найдем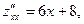

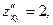
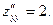
4. а) для точки 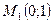имеем

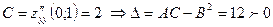
Так как 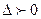и то по достаточному условию экстремума функция 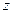имеет в точке 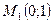минимум, причем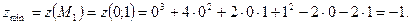

б) для точки 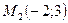имеем

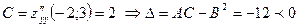
Так как 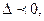то экстремум в точке 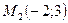отсутствует.

Дата добавления: 2014-01-20