Тогда уравнение множественной линейной регрессии, связывающая величину чистого дохода у с оборотом капитала х1 и использованным капиталом х2 имеет вид имеет вид

. (1.5)

На следующем этапе, в соответствии с заданием необходимо определить степень связи объясняющих переменных х₁ и х₂ с зависимой переменной у, используя коэффициенты эластичности. Коэффициенты эластичности для модели множественной линейной регрессии определяется в виде:

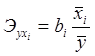. (1.6)

Тогда

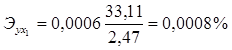. (1.7)

Следовательно, при изменении оборота капитала 1% величина чистого дохода копании изменяется на 0,0008%. .

При изменении использованного капитала на 1% величина чистого дохода компании изменяется на 0,56%.

На третьем этапе исследования необходимо оценить статистическую значимость коэффициентов регрессии с помощью t – критерия и нулевую гипотезу о значимости уравнения с помощью F – критерия.

Технология оценки статистической значимости коэффициентов регрессии также основывается на проверке нулевой гипотезы о не значимости коэффициентов регрессии. При этом проверяется выполнение условия:

если t_т > t_крит, то нулевая гипотеза отвергается, и коэффициент регрессии принимается значимым. Из рисунка 3.6 видно, что t_т для первого коэффициента регрессии равен -0,061, а для второго 5,5. Критическое значение t_крит при уровне значимости a = 0,05определяем с использованием статистической функции СТЬЮДРАСПОБР () рисунок. Входными параметрами функции является уровень значимости (Вероятность) и число степеней свободы. Для рассматриваемого примера число степеней свободы соответственно равно n-3 (так как, для двухфакторной модели множественной регрессии оценивается три параметра b₀ ,b₁, b₂) Тогда число степеней свободы равно10-3=7.

Рисунок 1.7. Окно статистической функции СТЬЮДРАСПОБР

Из рисунка 1.7 видно, что критическое значение t_крит =2,36.

Так как t_т < t_крит , для первого коэффициента регрессии (0,061< 2,36) то нулевая гипотеза не отвергается и объясняющая переменная х₁ является статистически незначимой и ее можно исключить из уравнения регрессии. И наоборот, для второго коэффициента регрессии t_т > t_крит (5,5 >2,36), и объясняющая переменная х₂ является статистически значимой.

Проверка значимости уравнения множественной регрессии в целом с использованием F – критерия аналогична проверке уравнения парной регрессии.

Из рисунка 3.6 следует, что F_т = 15,23. Критическое значение F – критерия F_крит, определяем с помощью использования статистической функции FРАСПОБР (). Для модели множественной регрессии с двумя переменными число степеней свободы соответственно равно 2 (две объясняющие переменные х₁ и х₂) и n-k –1(где k=2 – число объясняющих переменных). И второе число степеней свободы равно10-3= 7. Критическое значение F_крит = 4,74. Следовательно:

F_т > F_крит, (15,23 > 4,74), и уравнение регрессии в целом является значимым.

На последнем этапе исследования необходимо оценить качество уравнения посредством определения средней ошибки аппроксимации по зависимости (1.4). С этой целью представим таблицу 1.3 в виде вспомогательной таблицы 1.4. Тогда средняя ошибка аппроксимации составит:

. (1.8)

Таким образом:

Дата добавления: 2014-01-20