Лекция 4 множественная регрессия

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Например, при построении модели потребления того или иного товара от дохода исследователь предполагает, что в каждой группе дохода одинаково влияние на потребление таких факторов, как цена товара, размер семьи, ее состав. Вместе с тем исследователь никогда не может быть уверен в справедливости данного предположения. Для того чтобы иметь правильное представление о влиянии дохода на потребление, необходимо изучить их корреляцию при неизменном уровне других факторов. Прямой путь решения такой задачи состоит в отборе единиц совокупности с одинаковыми значениями всех других факторов, кроме дохода. Он приводит к планированию эксперимента - методу, который используется в химических, физических, биологических исследованиях.

Экономист в отличие от экспериментатора-естественника лишен возможности регулировать другие факторы. Поведение отдельных экономических переменных контролировать нельзя, т. е. не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. построить уравнение множественной регрессии:

y=a+b₁*x₁+b₂*x₂+…+b_p*x_p+ (9.1)

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия - один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, Включает в себя два круга вопросов; отбор факторов и выбор вида уравнения регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости).

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации R², который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других не учтенных в модели факторов оценивается как 1 - R² с соответствующей остаточной дисперсией S².

При дополнительном включении в регрессию р + 1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться

R²_p+1R²_p (9.2)

и

S²_p+1 S²_p (9.3)

Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор x_p+1не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй - на основе матрицы показателей корреляции определяют t-статистики для параметров регрессии.

Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы.

Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.

По величине парных коэффициентов корреляции может обнаруживаться лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т. е. имеет место совокупное воздействие факторов друг на друга.

Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).

Если рассматривается регрессия для расчета параметров, применяя МНК,

y=a+b*x+y*z+d*v+, (9.4)

то предполагается равенство

S_y=S_факт+S (9.5)

где S_y - общая сумма квадратов отклонений 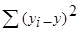, а S_факт - факторная (объясненная) сумма квадратов отклонений 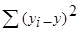, S- остаточная сумма квадратов отклонений .

В свою очередь, при независимости факторов друг от друга выполнимо равенство:

S_факт = S_x + S_z + S_v (9.6)

где S_x, S_z, S_v - суммы квадратов отклонений, обусловленные влиянием соответствующих факторов.

Если же факторы интеркоррелированы, то данное равенство нарушается.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:

· затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в "чистом" виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл;

· оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все не диагональные элементы были бы равны нулю.

Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных.

Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение коэффициента множественной детерминации к единице, тем сильнее проявляется мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной детерминации.

Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Например, при построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней, чтобы исключить влияние тенденции, или используются такие методы, которые сводят к нулю межфакторную корреляцию, т. е. переходят от исходных переменных к их линейным комбинациям, не коррелированных друг с другом (метод главных компонент).

Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т. е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие.

Рассматривается уравнение, включающее взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка (взаимодействие второго порядка).

Как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми, совмещенные уравнения регрессии ограничиваются взаимодействиями первого и второго порядков. Но и эти взаимодействия могут оказаться несущественными, поэтому нецелесообразно полное включение в модель взаимодействий всех факторов и всех порядков.

Совмещенные уравнения регрессии строятся, например, при исследовании эффекта влияния на урожайность разных видов удобрений (комбинаций азота и фосфора).

Решению проблемы устранения мультиколлинеарности факторов может помочь и переход к уравнениям приведенной формы. С этой целью в уравнение регрессии производится подстановка рассматриваемого фактора через выражение его из другого уравнения.

Пусть, например, рассматривается двухфакторная регрессия вида

у_х=а+b_i*x_i+b₂*X₂, дня которой факторы, xi и Х₂ обнаруживают высокую корреляцию. Если исключить один из факторов, то мы придем к уравнению парной регрессии. Вместе с тем можно оставить факторы в модели, но исследовать данное двухфакторное уравнение регрессии совместно с другим уравнением, в котором фактор рассматривается как зависимая переменная.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

· метод исключения;

· метод включения;

· шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты - отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

На первый взгляд может показаться, что матрица парных коэффициентов корреляции играет главную роль в отборе факторов. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать вопрос о целесообразности включения в модель того или иного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результатом.

Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6 - 7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F-критерий меньше табличного значения.

По существу эффективность и целесообразность применения эконометрических методов наиболее явно проявляются при изучении явлений и процессов, в которых зависимая переменная (объясняемая) подвержена влиянию множества различных факторов (объясняющих переменных). Множественная регрессия это уравнение связи с несколькими независимыми переменными. Позднее, правда, мы увидим, что эту независимость не следует понимать абсолютно. Необходимо исследовать какие объясняющие переменные можно считать независимыми в силу их незначительной связи между собой, а для каких это несправедливо. Но в качестве первого приближения, хорошо оправдывающегося во многих случаях и необходимого для понимания дальнейшего, мы изучим сначала этот более простой случай с независимыми объясняющими переменными

Каким образом отбираются факторы, входящие в модель множественной регрессии? Прежде всего, эти факторы должны поддаваться количественному измерению. Может оказаться, что необходимо включить в модель (уравнение) некий качественный фактор, который не имеет количественного измерения. В этом случае следует добиться количественной определенности такого качественного фактора, т.е. ввести некоторую шкалу оценки данного фактора и по ней оценить его. Далее факторы не должны иметь явно выраженной и к тому же сильной взаимосвязи (имеется в виду общая стохастическая связь, или корреляция), т.е. не быть интеркоррелированы.

Тем более, не допустимо наличие между факторами явной функциональной связи! В случае факторов с высокой степенью интеркорреляции система нормальных уравнений может оказаться плохо обусловленной, т.е. независимо от выбора численного метода ее решения получающиеся оценки коэффициентов регрессии будут неустойчивыми и ненадежными. Более того, при наличии высокой корреляции между факторами крайне трудно, практически невозможно определить изолированное влияние факторов на результативный признак, а сами параметры уравнения регрессии оказываются неинтерпретируемы.

Для оценки параметров уравнения множественной регрессии также как и для оценки таких параметров в простейшем случае парной однофакторной регрессии используется метод наименьших квадратов (МНК). Соответствующая система нормальных уравнений имеет структуру аналогичную той, которая была в модели однофакторной регрессии. Но теперь является более громоздкой, и для ее решения можно применять известный из линейной алгебры метод определителей Краммера.

Если парная регрессия (однофакторная) может дать хороший результат, в случае когда влиянием других факторов можно пренебречь, то исследователь не может быть уверен в справедливости пренебрежения влиянием прочих факторов в общем случае. Более того, в экономике в отличие от химии, физики и биологии затруднительно использовать для преодоления этой трудности методы планирования эксперимента, ввиду отсутствия в экономике возможности регулирования отдельных факторов! Поэтому особенно большое значение приобретает попытка выявления влияния прочих факторов с помощью построения уравнения множественной регрессии и изучения такого уравнения.

Анализ модели множественной регрессии требует разрешения двух весьма важных новых вопросов. Первым является вопрос разграничения эффектов различных независимых переменных. Данная проблема, когда она становится особенно существенна носит название проблемы мультиколлинеарности. Вторая, не менее важная проблема заключается в оценке совместной (объединенной) объясняющей способности независимых переменных в противоположность влиянию их индивидуальных предельных эффектов.

С этими двумя вопросами связана проблема спецификации модели. Дело в том, что среди нескольких объясняющих переменных имеются оказывающие влияние на зависимую переменную и не оказывающие такового влияния. Более того, некоторые переменные могут и вовсе не подходить для данной модели. Поэтому необходимо решить какие переменные следует включать в модель (уравнение). А какие переменные напротив необходимо исключить из уравнения. Так, если в уравнение не вошла переменная, которая по природе исследуемых явлений и процессов в действительности должна была быть включена в эту модель, то оценки коэффициентов регрессии с довольно большой вероятностью могут оказаться смещенными. При этом рассчитанные по простым формулам стандартные ошибки коэффициентов и соответствующие тесты в целом становятся некорректными.

Если же включена переменная, которая не должна присутствовать в уравнении, то оценки коэффициентов регрессии будут несмещенными, но с высокой вероятностью окажутся неэффективными. Также оказывается в этом случае, что рассчитанные стандартные ошибки окажутся в целом приемлемы, но из-за неэффективности регрессионных оценок они станут чрезмерно большими.

Особого внимания заслуживают так называемые замещающие переменные. Часто оказывается, что данные по какой либо переменной не могут быть найдены или что определение таких переменных столь расплывчато, что непонятно как их в принципе измерить. Другие переменные поддаются измерению, но таковое весьма трудоемко и требует много времени, что практически весьма неудобно. Во всех этих и иных случаях приходится использовать некоторую другую переменную, вместо вызывающей описанные выше затруднения. Такая переменная называется замещающей, но каким условиям она должна удовлетворять? Замещающая переменная должна выражаться в виде линейной функции (зависимости) от неизвестной (замещаемой) переменной и наоборот последняя также связана линейной зависимостью с замещающей переменной. Важно, что сами коэффициенты линейной зависимости неизвестны. Иначе всегда можно выразить одну переменную через другую и вовсе не использовать замещающей переменной. Оставаясь неизвестными коэффициенты являются обязательно постоянными величинами. Бывает и так, что замещающая переменная используется непреднамеренно (неосознанно).

Включаемые в уравнение множественной регрессии факторы должны объяснить вариацию зависимой переменной. Если строится модель с некоторым набором факторов, то для нее рассчитывается показатель детерминации, который фиксирует долю объясненной вариации результативного признака (объясняемой переменной) за счет рассматриваемых в регрессии факторов. А как оценить влияние других не учтенных в модели факторов? Их влияние оценивается вычитанием из единицы коэффициента детерминации, что и приводит к соответствующей остаточной дисперсии.

Таким образом, при дополнительном включении в регрессию еще одного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит и данные показатели практически недостаточно значимо отличаются друг от друга, то включаемый в анализ дополнительный фактор не улучшает модель и практически является лишним фактором.

Если модель насыщается такими лишними факторами, то не только не снижается величина остаточной дисперсии и не происходит увеличения показателя детерминации, но более того снижается статистическая значимость параметров регрессии по критерию Стьюдента вплоть до статистической незначимости!

Вернемся теперь к уравнению множественной регрессии с точки зрения различных форм, представляющих такое уравнение. Если ввести стандартизованные переменные, представляющие собой исходные переменные, из которых вычитаются соответствующие средние, а полученная разность делится на стандартное отклонение, то получим уравнения регрессии в стандартизованном масштабе. К этому уравнению применим МНК. Для него из соответствующей системы уравнений определяются стандартизованные коэффициенты регрессии b (бета-коэффициенты). В свою очередь коэффициенты множественной регрессии просто связаны со стандартизованными бета-коэффициентами, именно коэффициенты регрессии получаются из бета-коэффициентов умножением последних на дробь, представляющую собой отношение стандартного отклонения результативного фактора к стандартному отклонению соответствующего объясняющего переменного.

В простейшем случае парной регрессии стандартизованный коэффициент регрессии это не что иное, как линейный коэффициент корреляции. Вообще стандартизованные коэффициенты регрессии показывают на сколько стандартных отклонений изменится в среднем результат, если соответствующий фактор изменится на одно стандартное отклонение при неизменном среднем уровне других факторов. Кроме того, поскольку все переменные заданы как центрированные и нормированные, все стандартизованные коэффициенты регрессии сравнимы между собой. Поэтому сравнивая их между собой, можно ранжировать факторы по силе их воздействия на результат. Следовательно можно использовать стандартизованные коэффициенты регрессии для отсева факторов с наименьшим влиянием на результат просто по величинам соответствующих стандартизованных коэффициентов регрессии.

Теснота совместного влияния факторов на результат оценивается с помощью индекса множественной корреляции, который дается простой формулой: из единицы вычитается отношение остаточной дисперсии к дисперсии результативного фактора, а из полученной разности извлекается квадратный корень:

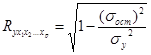(9.7)

Его величина лежит в пределах от 0 до 1 и при этом больше или равна максимальному парному индексу корреляции. Для уравнения в стандартизованном виде (масштабе) индекс множественной корреляции записывается еще проще, т.к. подкоренное выражение в данном случае является просто суммой попарных произведений бета-коэффициентов на соответствующие парные индексы корреляции:

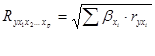(9.8)

Т.о. в целом качество построенной модели оценивают с помощью коэффициента, или индекса детерминации как показано выше. Этот коэффициент множественной детерминации рассчитывается как индекс множественной корреляции, а иногда используют скорректированный соответствующий индекс множественной детерминации, который содержит поправку на число степеней свободы. Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера. Имеется также частный F-критерий Фишера, оценивающий статистическую значимость присутствия каждого из факторов в уравнении.

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению корня квадратного из величины соответствующего частного критерия Фишера, или что то же самое нахождения величины отношения коэффициента регрессии к среднеквадратической ошибке коэффициента регрессии.

При тесной линейной связанности факторов, входящих в уравнение множественной регрессии, возможно возникновение проблемы мультиколлинеарности факторов. Количественным показателем явной коллинеарности двух переменных является соответствующий линейный коэффициент парной корреляции между этими двумя факторами. Две переменные явно коллинеарны, если этот коэффициент корреляции больше или равен 0,7. Но это указание на явную коллинеарность факторов совершенно не достаточно для исследования общей проблемы мультиколлинеарности факторов, т.к. чем сильнее мультиколлинеарность (без обязательного наличия явной коллинеарности) факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК.

Более эффективным инструментом оценки мультиколлинеарности факторов является определитель матрицы парных коэффициентов корреляции между факторами. При полном отсутствии корреляции между факторами матрица парных коэффициентов корреляции между факторами просто единичная матрица, ведь все недиагональные элементы в этом случае равны нулю. Напротив, если между факторами имеется полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен 0. Следовательно, можно сделать вывод, что чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. Чем ближе к 1 этот определитель, тем меньше мультиколлинеарность факторов.

Если известно, что параметры уравнения множественной регрессии линейно зависимы, то число объясняющих переменных в уравнении регрессии можно уменьшить на единицу. Если действительно использовать подобный прием, то можно повысить эффективность оценок регрессии. Тогда, имевшаяся ранее мультиколлинеарность, может быть смягчена. Даже если такая проблема и отсутствовала в исходной модели, то все равно выигрыш в эффективности может привести к улучшению точности оценок. Естественно такое улучшение точности оценок отражается стандартными ошибками их. Сама линейная зависимость параметров называется также линейным ограничением.

Помимо уже рассмотренных вопросов нужно иметь в виду, что при использовании данных временного ряда не обязательно требовать выполнения условия, что на текущее значение зависимой переменной влияют только текущие же значения объясняющих переменных. Именно можно ослабить это требование и исследовать в какой степени проявляется запаздывание соответствующих зависимостей и такое влияние его. Спецификация запаздываний для конкретных переменных в данной модели называется лаговой структурой (от слова лаг – запаздывание). Такая структура бывает важным аспектом модели, и сама может выступать в роли спецификации переменных модели. Поясним сказанное простым примером. Можно считать, что люди склонны соотносить свои расходы на жилье не с текущими расходами или ценами, а с предшествующими, например, за прошлый год.

Дата добавления: 2014-01-20