И проблема идентификации

ЛЕКЦИЯ 5. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Сложные системы и процессы в них, как правило, описываются не одним уравнением, а системой уравнений. При этом между переменными имеются связи, так что, по крайней мере, некоторые из таких связей между переменными требуют корректировки МНК для адекватного оценивания параметров модели (параметров системы уравнений). Удобно сначала рассмотреть оценивание системы, в которой уравнения связаны только благодаря корреляции между ошибками (остатками) в разных уравнениях системы. Такая система называется системой внешне не связанных между собой уравнений:

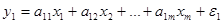
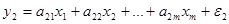(5.1)

………………………………

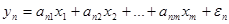
В такой системе каждая зависимая переменная рассматривается как функция одного и того же набора факторов, правда этот набор факторов вовсе не обязан быть представлен весь целиком во всех уравнениях системы, а может варьировать от одного уравнения к другому. Можно рассматривать каждое уравнение такой системы независимо от остальных и применять для оценивания его параметров МНК. Но в практически важных задачах описываемые отдельными уравнениями зависимости представляют объекты и взаимодействие между этими объектами, которые находятся в одной общей среде. Наличие этой единой экономической среды обусловливает взаимосвязи между объектами и соответствующее взаимодействие, за что отвечают в данном случае остатки (корреляция между ошибками). Поэтому объединение уравнений в систему и применение ОМНК для ее решения существенно повышает эффективность оценивания параметров уравнений.

Более общей является модель так называемых рекурсивных уравнений, когда зависимая переменная одного уравнения выступает в роли фактора х, оказываясь в правой части другого уравнения системы. При этом каждое последующее уравнение системы (зависимая переменная в правой части этих уравнений) включает в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором их собственных факторов х. Здесь опять каждое уравнение системы может рассматриваться независимо, но то же эффективнее рассматривать взаимосвязь через остатки и применять ОМНК.

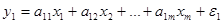
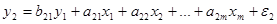
(5.2)

……………………………………………………

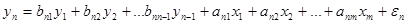
Наконец, общим и самым полным является случай системы взаимосвязанных уравнений. Такие уравнения еще называют одновременными, или взаимозависимыми. Также это система совместных одновременных уравнений. Здесь уже одни и те же переменные рассматриваются одновременно как зависимые в одних уравнениях и в то же самое время – как независимые в других уравнениях системы. Такая форма модели называется структурной формой модели. Теперь уже нельзя рассматривать каждое уравнение системы по отдельности (как самостоятельное), так что для оценки параметров системы традиционный МНК неприменим!

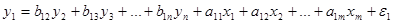
(5.3)

……………………………………………………….

Для этой структурной формы модели существенное значение получает деление переменных модели на два различных класса. Эндогенные переменные – взаимозависимые переменные, которые определяются внутри модели (внутри самой системы) и обозначаются у. Второй класс это экзогенные переменные – независимые переменные, которые определяются вне системы и обозначаются как х. Кроме того, вводится также понятие предопределенных переменных. Под ними понимаются экзогенные переменные системы и лаговые эндогенные переменные системы (лаговые это переменные, относящиеся к предыдущим моментам времени).

Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты, которые называются структурными коэффициентами модели. Можно представить систему (модель) в другой форме. Именно записать ее как систему, в которой все эндогенные переменные линейно зависят уже только от экзогенных переменных. Иногда практически то же формулируют несколько более общим формально образом. То есть требуют, чтобы эндогенные переменные линейно зависели только от всех предопределенных переменных системы (т.е. экзогенных и лаговых эндогенных переменных системы). В любом из этих двух случаев такая форма называется приведенной формой модели. Приведенная форма уже ничем внешне не отличается от системы независимых уравнений.

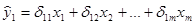
(5.4)

……………………………

Ее параметры оцениваются по МНК. После чего несложно оценить и значения эндогенных переменных с помощью значений экзогенных переменных. Но коэффициенты приведенной формы модели являются нелинейными функциями коэффициентов структурной формы модели. Таким образом, получение оценок параметров структурной формы модели по параметрам приведенной формы технически является не столь уж простым.

Нужно отметить также, что приведенная форма модели аналитически уступает структурной форме модели, т.к. именно в структурной форме модели имеется взаимосвязь между эндогенными переменными. В приведенной форме модели отсутствуют оценки взаимосвязи между эндогенными переменными. С другой стороны в структурной форме модели в полном виде имеется большее количество параметров, чем в приведенной форме модели. И это большее количество параметров, которые требуется определить по меньшему числу определяемых в приведенной форме параметров, невозможно однозначно найти, если только не ввести определенные ограничения на сами структурные коэффициенты.

Описанная только что наиболее общая модель – система взаимозависимых уравнений – получила название системы совместных, одновременных уравнений. Эта структурная форма модели подчеркивает, что в такой системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. Важным примером такой модели служит следующая простая модель динамики и заработной платы

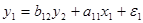(5.5)

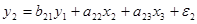
В этой модели левые части первого и второго уравнений системы это темп изменения месячной заработной платы и темп изменения цен. Переменные, стоящие в правых частях уравнений, х₁ – процент безработных, х₂ – темп изменения постоянного капитала, х₃ – темп изменения цен на импорт сырья.

Что касается структурной модели, то она позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Поэтому следует в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Тогда меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменные.

Таким образом, существуют две различные формы моделей, которые описывают одну ситуацию, но имеют определенные преимущества в контексте решения различных проблем, различных аспектов этой ситуации. Следовательно, нужно уметь устанавливать и поддерживать должное соответствие между этими двумя формами моделей. Так при переходе от структурной формы модели к приведенной форме модели возникает проблема идентификации – единственности соответствия между приведенной и структурной формами модели. По возможности идентифицируемости структурные модели делятся на три вида.

Модель идентифицируема, если все структурные коэффициенты модели однозначно определяются по коэффициентам приведенной формы модели. При этом число параметров в обеих формах модели одинаково.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов. Тогда структурные коэффициенты не могут быть определены и оценены через коэффициенты приведенной формы модели.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В таком случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически всегда решаема, однако для этого используются специальные методы вычисления параметров.

Следует подчеркнуть опять, что деление переменных на эндогенные и экзогенные зависит от содержания модели, а не от ее формальных особенностей. Именно интерпретация определяет какие переменные считать эндогенными, а какие – экзогенными. При этом предполагается, что эндогенные переменные некоррелированы с ошибкой для каждого уравнения. Тогда как экзогенные переменные (они стоят в правых частях уравнений) как правило, имеют ненулевую корреляцию с ошибкой в соответствующем уравнении. Для приведенной формы уравнений (в отличие от структурной формы) в каждом уравнении экзогенная переменная некоррелирована с ошибкой. Именно поэтому МНК для ее параметров дает состоятельные оценки. А сам такой способ оценки параметров (уже структурных коэффициентов) с помощью оценок коэффициентов приведенной формы и МНК называется косвенным методом наименьших квадратов. Использование косвенного метода наименьших квадратов заключается просто в составлении приведенной формы, для определения численных значений параметров каждого уравнения посредством обычного МНК. После этого с помощью алгебраических преобразований переходят опять к исходной структурной форме модели и получают тем самым численные оценки структурных параметров.

Итак, косвенный метод наименьших квадратов применяется для решения идентифицируемой системы. А как следует поступать в случае сверхидентифицируемой ситстемы? В этом случае применяется двухшаговый метод наименьших квадратов.

Двухшаговый МНК (ДМНК) использует следующую центральную идею: на основе приведенной формы модели получают для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Затем они подставляются вместо фактических значений и применяют обычный МНК к структурной форме сверхидентифицируемого уравнения. В свою очередь сверхидентифицируемая структурная модель может быть двух типов. Либо все уравнения системы сверхидентифицируемы. Либо же система содержит наряду со сверхидентифицируемыми также и точно идентифицируемые уравнения. В первом случае, если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

Структурная модель это система совместных уравнений, каждое из которых нужно проверять на идентификацию. Вся модель считается идентифицируемой, если идентифицируемо каждое уравнение системы. Если неидентифицируемо, хотя бы одно из уравнений системы, то вся система неидентифицируема. Сверхидентифицируемая модель должна содержать хотя бы одно сверхидентифицируемое уравнение. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в во всей системе в целом, равнялось числу эндогенных переменных в данном уравнении без одного.

Необходимое условие идентификации это выполнение счетного правила. Если число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе, увеличенное на единицу, равно числу эндогенных переменных в уравнении, то уравнение идентифицируемо. Если меньше – то неидентифицируемо. Если больше – то сверхидентифицируемо.

Это простое условие является всего лишь необходимым. Оно не достаточно. Достаточным является более сложное условие идентификации. Оно накладывает определенные условия на коэффициенты матриц параметров структурной модели.

Именно уравнение идентифицируемо, если определитель матрицы, составленной из коэффициентов при переменных, которые отсутствуют в исследуемом уравнении, но наличествуют в других уравнениях системы не равен нулю и при этом ранг этой матрицы не менее числа эндогенных переменных системы без единицы.

Помимо уравнений, параметры которых необходимо оценить, в эконометрических моделях используют и балансовые тождества переменных, коэффициенты, при которых равны по модулю единице. Понятно, что само тождество не нужно проверять на идентификацию, т.к. коэффициенты в тождестве известны. Но в проверке самих структурных уравнений системы тождества участвуют. Наконец, ограничения могут накладываться также на дисперсии и ковариации остаточных величин.

Вообще говоря, наиболее общим является оценивание по методу максимального правдоподобия. Этот метод при большом количестве уравнений достаточно трудоемок с вычислительной точки зрения. Несколько легче реализуется метод максимального правдоподобия при ограниченной информации, который называется методом наименьшего дисперсионного отношения. Но и он значительно сложнее ДМНК, так что ДМНК остается доминирующим вместе с некоторыми дополнительными методами.

Дадим (для интересующихся этим вопросом) несколько более полное разъяснение по методу максимального правдоподобия (ММП). Пусть имеется непрерывная случайная переменная, у которой нормальное распределение, известно стандартное отклонение, равное единице и неизвестно среднее. Нам же требуется найти значение среднего, которое максимизирует плотность вероятности для заданного наблюдения х₁. Далее эта схема обобщается для случая уже не одного, а множества наблюдений и соответствующих значений х_i. При этом получаем уже многомерную функцию распределения в виде произведения соответствующих одномерных плотностей вероятностей. Такую функцию можно использовать для проведения теста на отношение правдоподобия. Но есть и весомые аргументы, снижающие привлекательность применения ММП, помимо уже отмеченной вычислительной сложности. Как правило выборки являются малыми, так что методы с хорошими свойствами для больших выборок, не обязаны обладать таковыми для малых выборок. Далее для моделей с трендом ММП также как и МНК может быть достаточно уязвим. Имеется также ограничение на асимптотическое распределение случайного члена.

Применение систем эконометрических уравнений представляет собой не простую задачу. Проблемы здесь происходят из-за ошибок спецификации. Основной областью применения эконометрических моделей является построение макроэкономических моделей экономики целой страны. Это главным образом мультипликаторные модели кейнсианского типа. Более совершенными по сравнению со статическими моделями являются динамические модели экономики, которые содержат в правой части лаговые переменные и учитывают тенденцию развития (фактор времени). Значительные трудности создает невыполнение условия независимости факторов, которое в корне нарушается в системах одновременных (взаимозависимых) уравнений.

Использование корреляционно-регрессионного анализа в контексте структурного моделирования это попытка подойти к выделению и измерению причинных связей переменных. Для этого следует сформулировать гипотезы о структуре влияний и корреляции. Такая система причинных гипотез и соответствующих взаимосвязей изображается графом, вершины которого это переменные (причины или следствия), а дуги это причинные отношения. Далее верификация гипотез требует установления соответствия между графом и системой уравнений, описывающей этот граф.

Структурные модели эконометрики представляются системой линейных по отношению к наблюдаемым переменным уравнений. Если алгебраическая система соответствует графу без контуров (петель), то она является рекурсивной системой. Такая система позволяет рекуррентно определять значения входящих в нее переменных. В ней в уравнения для признака включаются все переменные, кроме тех переменных, которые расположены выше него по графу. Соответственно формулировка гипотез в структуре рекуррентной модели довольно проста, при условии использования данных динамики. Рекуррентная система уравнений позволяет определить полные и частные коэффициенты влияния факторов. Коэффициенты полного влияния измеряют значение каждой переменной в структуре. Структурные модели позволяют оценить полное и непосредственное влияние переменных, прогнозировать поведение системы, рассчитывать значения эндогенных переменных.

Если нужно всего лишь уточнить характер связей переменных, то используют метод путевого анализа (путевых коэффициентов). В основе его лежит гипотеза об аддитивном характере (аддитивность и линейность) связей между переменными. К сожалению применение путевого анализа в социально-экономических исследованиях затруднено тем, что не всегда линейная зависимость удовлетворительно выражает все разнообразие причинно-следственных связей в реальных системах. Значимость результатов анализа определяется правильностью построения максимально связного графа и соответственно изоморфной математической модели в виде системы уравнений. В то же время важным достоинством путевого анализа является возможность производить декомпозицию корреляций.

Дата добавления: 2014-01-20