Основы теории вероятностей. Случайное событие, случайная величина, вероятность

Спортивная метрология как учебная дисциплина

Введение

Слово “метрология” в переводе с древнегреческого означает “наука об измерениях” (метрон – мера, логос – слово, наука). Метрология возникла из-за большого разнообразия единиц измерения одних и тех же величин и необходимости их приведения к единству и обеспечения точности измерения.

Основной задачей общей метрологии является обеспечение единства и точности измерений. Спортивная метрология как научная дисциплина представляет собой часть общей метрологии.

РАЗДЕЛ 1. Теоретические основы спортивной метрологии и математико-статистические методы в физическом воспитании и спорте

Спортивная метрология – это наука об измерениях в физическом воспитании и спорте.

Предметом спортивной метрологии является комплексный контроль в физическом воспитании и спорте и использование его результатов в планировании подготовки спортсменов.

Традиционно метрология занималась измерением только физических величин. К ним относятся: длина, масса, время, температура, сила электрического тока, сила света и количество вещества. Некоторые из этих величин подлежат измерению и в физической культуре, например, время, масса, длина, сила. Но более всего специалистов этой области интересуют разнообразные показатели нефизической природы – педагогические, психологические, социальные, биологические. На современном этапе созданы методы, позволяющие измерять такие показатели.

Теория вероятностей – раздел математики, который оперирует случайными величинами и имеет дело со случайными событиями.

Случайное событие – событие, которое случается с определенной вероятностью во время проведения испытания, т.е. оно не закономерно, его нельзя достоверно предсказать заранее. Например, баскетболист кидает мяч в кольцо. Это испытание, в результате которого мяч попадает или не попадает в кольцо. Его попадание в кольцо является случайным событием. Вероятность этого события зависит от мастерства спортсмена.

Случайная величина – такая величина, которая претерпевает случайные изменения от испытания к испытанию (от измерения к измерению). В зависимости от возможных значений случайная величина может быть дискретной или непрерывной. Например, при бросании игральной кости могут выпадать только целые значения (от 1 до 6) – это дискретная случайная величина; а время пробега спортсменом дистанции может изменяться плавно – это непрерывная случайная величина.

Существует статистическое и классическое определение вероятности. Рассмотрим статистическое определение.

Будем фиксировать число испытаний, в результате которых появилось событие А. Всего было проведено N испытаний. В результате этих испытаний событие А наступило n_N раз. Число n_N называется частотой события, а отношение
n_N /N – частостью (относительной частотой) события А. (События в теории вероятностей принято обозначать заглавными латинскими буквами А, В, С, ….) Если мы будем увеличивать число испытаний N до бесконечности, то заметим, что относительная частота события А стремится к какому-то определенному числу, которое и называется вероятностью события А и обозначается Р(А). Математически это обозначается:

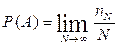
Так как n_N≥0, то Р(А) ≥0 и т.к. n_N≤N, то Р(А) ≤1, т.е. значение вероятности может находиться в пределах 0≤Р(А) ≤1.

Экспериментально это проверить нельзя, т.к. на практике невозможно провести бесконечное количество испытаний.

Далее следует классическое определение вероятности по Лапласу, которое пришло к нам из области азартных игр, где теория вероятностей применялась для определения перспективы выигрыша.

Пусть испытание имеет n возможных исходов, т.е. отдельных событий, могущих появиться в результате данного испытания; причем при каждом повторении испытания возможен один и только один из этих исходов. Таким образом, все n исходов несовместимы. Кроме того, по условиям испытаний нет никаких оснований предполагать, что один из исходов появляется чаще других, т.е. все исходы являются равновозможными.

Допустим теперь, что при n равновозможных исходах интерес представляет только некоторое событие А, появляющееся при каждом из m исходов и не повторяющееся при остальных n-m исходах. Тогда принято говорить, что в данном испытании имеется n случаев, из которых m благоприятствуют появлению события А.

Вероятность события А в такой схеме равна отношению числа случаев, благоприятствующих события А, к общему числу всех равновозможных несовместимых случаев:

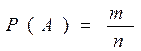
Например, при бросании игральной кости может выпадать 1, 2, 3, 4, 5 или 6 очков. Все исходы равновозможны. Здесь n=6. Если нас интересует событие, заключающееся в выпадении 6 очков, то этому благоприятствует только 1 исход, т.е. m=1. В этом случае вероятность выпадения 6-ти очков Р(А)=1/6. В том случае, если нас будет интересовать выпадение любого четного числа (2, 4, 6), то в этом случае m=3. И тогда Р(А)=3/6=1/2=0,5.

Дата добавления: 2014-01-20