Изменение сроков инвестиционных платежей и дохода производства

Резервы, факторы и основные направления повышения эффективности проекта

Резервы и пути повышения эффективности проектного решения

Таблица 5.1

№ п.п.	Факторы	Пути повышения	Резервы
Выигрыш времени	Выигрыш денеж­ных средств
Уско­рить начало эксплу-ат. про­екта	Увели­чить срок эксплуат проекта	Опти­ми­зация сроков вложе­ний	Мак­сими­зация дохода	Мини­миза­ция вложе­ний
	Материально технический	1.1. Производство высококачественной продукции.		+		+
		1.2. Использование прогрессивной тех­нологии, техники и материалов.		+		+
		1.3. Повышение конкурентоспособности продукции		+		+
		1.4. Создание прогрессивного проект­ного решения, минимизирующего капи­таловложения и т.д.
	Организационные	2.1. Совершенствование освоения нового дела	+		+
		2.2. Построение сетевого графика вы­полнения строительно-монтажных работ	+		+
		2.3. Своевременное создание материаль­ных запасов и т.д.	+		+
	Управленческие	3.1. Согласование и координация работ в области создания и освоения нового дела	+		+
		3.2. Разработка оптимальной маркетин­говой стратегии		+		+
		3.3. Выбор нового прогрессивного дела в условиях инфляции и т.д.				+
	Социально-экономические	4.1. Стимулирование ускорения строи­тельства и освоения нового дела	+		+		+
		4.2. Совершенствование оплаты труда в процессе эксплуатации нового дела и т.д.				+
	Административные	5.1. Обоснование и выбор прогрессив­ных управленческих решений	+	+	+	+	+
		5.2. Обеспечение и контроль трудовой, производственной и технологической дисциплины и т.д.	+	+	+	+	+

Примечание: так «+» означает возможность использования данного фактора и направления для реализации конкретного резерва повышения эффективности инвестиций.

Как видно из таблицы, реализация резервов возможна за счет использования огромного количества разнообразных мероприятий, а здесь приведены только некоторые из них.

Запишем суммарную величину инвестиционных платежей за период — t_И. Это будут затраты, которые можно представить в следующем виде.

где К_i — величина вложений в проект в i-ом временном интервале;

q — внутренняя норма доходности проекта;

t_И — период от начала инвестирования до конца инвестиционного периода.

Допустим, что все К_i равны между собой. Тогда их можно вынести за знак суммы:

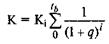
Полученное выражение можно представить как сумму убывающей геометрической прогрессии, величину которой можно определить по формуле

В том случае, когда вложения по временным интервалам не равны между собой, как это часто бывает на практике, следует поступить следующим образом. Вместо величины — К_i можно всегда подобрать такое число, которое обеспечит тот же результат расчета, который можно получить с помощью одинаковых вложений по тем же временным интервалам и при одинаковой норме доходности. Обозначим такую величину вложений через — К_Э. Она будет означать вложения в инвестиционный проект, эквивалентные реальным. По своей величине эквивалентные вложения будут отличаться от фактических вложений, но их сумма точно совпадает с суммарной величиной фактических вложений. И это позволяет сделать следующий шаг на пути к анализу резервов повышения эффективности инвестиционных вложений.

Запишем теперь формулу суммарных вложений с применением эквивалентных вложений:

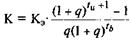(5.5)

Проведем проверочный расчет суммарных вложений при условии, что вложения по временным интервалам составляют — К₀ = 8 ед., К₁ = 10 ед., К₂ = 12 ед., К₃ = 14 ед., а внутренняя норма доходности — q = 0,1.

Рассчитаем дисконтированные инвестиционные вложения:

К= 8: 1,1⁰+10: 1,1¹ + 12: 1,1² + 14: 1,1³ = = 8 + 9,091 + 9,917 + 9,562 = 36,57

Полученную сумму приравняем к последней формуле (5.5) и затем определим величину эквивалентных вложений. Эта расчетная операция обеспечит следующий результат

36,57 = К_Э-(1,1⁴- 1): 0,1: 1.1³= 3,487 • К_Э

Тогда эквивалентные вложения составят:

К_Э = 36,57: 3,487 = 10,488 ед.

Эта величина вложений в каждом временном интервале, обеспечит тот же суммарный результат, который получается при различных вложениях в те же временные интервалы. Таким образом, удается получить точную сумму дисконтирования различных во времени вложений, но только заменив их постоянными вложениями по тем же интервалам времени.

Теперь проведем аналогичную операцию с доходной составляющей проекта, которая возникает с началом его эксплуатации, т.е. по истечении времени — t_H и продолжается в течение времени — t_Э. Следовательно, доход за период эксплуатации проекта надо дисконтировать к начальному моменту его функционирования. Эту операцию можно представить в следующем виде

где Д — суммарная величина дохода за весь срок эксплуатации проекта;

Д_i — доход предприятия в i-ом временном интервале.

Теперь заменим всю совокупность различных значений дохода по временным интервалам эквивалентным доходом, который будет одинаковым для всех интервалов:

где Д_Э — эквивалентный доход, одинаковый во всех временных интервалах.

Выражение, стоящее под знаком суммы, представляет собой сумму членов геометрической прогрессии, величину которой можно рассчитать по следующей формуле:

(5.6)

Для определения величины внутренней нормы доходности необходимо приравнять между собой формулы (5.5) и (5.6):

В результате преобразований полученное выражение будет иметь следующий вид:

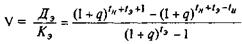(5.7)

где V — коэффициент отношения эквивалентных значений дохода и инвестиционных вложений, взятых за один временной интервал.

Как вытекает из формулы (5.7), фиксированный коэффициент V при заранее установленных временных параметрах (t_И, t_H и t_Э) позволяет не только определить величину внутренней нормы доходности (q), но и прогнозировать, как она изменится в процессе варьирования величинами отдельных временных характеристик.

Прежде, чем перейти непосредственно к анализу существующих резервов повышения эффективности инвестиций, произведем проверку полученной формулы (5.7).

Пусть инвестиционный проект имеет следующие временные характеристики:

· инвестиционный период — t_И = 2 временных интервала;

· период от начала инвестирования до начала эксплуатации — t_Н ⁼ 2;

· эксплуатационный период — t_Э = 3 временных интервала.

Кроме того примем:

· величина инвестиционных вложений в каждом временном интервале составляет — К_Э = 1000 ден. ед.;

· величина дохода в каждом временном интервале — Д_Э = = 1331 ден. ед.

Подставим зафиксированные исходные данные в формулу (5.7)

Если разрешить полученное выражение относительно неизвестного значения внутренней нормы доходности (q), то получим — q = 0,1.

Действительно, V = (1,1⁶ - 1.1³): (1,1³ - 1) = 1,331

Таким образом, полученный результат идентичен коэффициенту — V, т.е. формула (5.7) точно отражает экономическую сущность происходящих процессов и явлений в инвестировании и ею, поэтому, можно воспользоваться для обоснования резервов повышения эффективности инвестиций.

Первый временной параметр, который подлежит исследованию — это инвестиционный период — t_И. Предположим, что:

tи = 4; t_H = 3; t₃ = 7; Д_Э = 1250 ден. ед.; К_Э = 1000 ден. ед.

Произведем расчет внутренней нормы доходности и сведем полученные результаты в таблицу.

Исходя из полученных результатов, можно сделать ряд интересных выводов. Во-первых, изменения продолжительности инвестиционного периода, реализуемые через параметр — t_H, рассматриваются здесь при сохранении всех прочих параметров, за исключением коэффициента — V.

Таблица 5.2

Дата добавления: 2014-01-20