Лекция 8. Рассмотрим смешанные граничные условия (вариант С)

Рассмотрим смешанные граничные условия (вариант С).

Рис. 23. Узловые точки для варианта граничных условий С

При x=0 (точка 1) статическое граничное условие N(0)=0, а значит

, в конечно-разностной форме это выражение имеет вид:

(2.1.29)

Такая запись накладывает дополнительные условия на область решения. Вводим «законтурную» точку (точка 0) и статическое граничное условие определяется в этом случае соотношением:

(2.1.30)

Теперь никаких дополнительных условий не накладывается. Точка 1 становится внутренней и система конечноразностных уравнений запишется так (из правого геометрического граничного условия следует, что u₅=0):

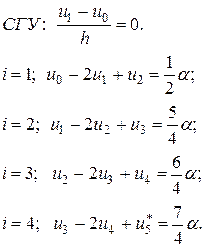(2.1.31)

Следует обратить внимание на то, что для левой крайней точки берется половина значения функции нагрузки, т. к. слева от нее стержень не существует.

Производим прямой ход исключения неизвестных верху:

(2.1.32)

Выполняем обратный ход, раскрывая a и приводя полученные значения к размерности точного решения:

(2.1.33)

Осуществим переход к усилиям в рамках МКР

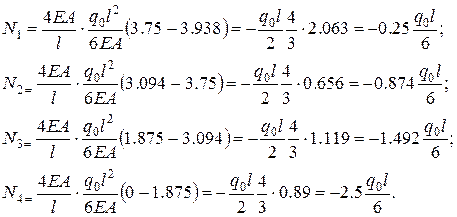(2.1.34)

Воспользуемся дифференцирующей матрицей

(2.1.35)

Результаты расчета приведены в таблице 7 и на графике (рис. 24, 25). Звездочкой отмечены усилия, полученные в рамках МКР, двумя звездочками – усилия, полученные с помощью дифференцирующей матрицы.

Таблица 7

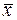
		0.25	0.5	0.75	1.0
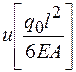
	3.938 (4)	3.750 (3.797)	3.094 (3.125)	1.875 (1.891)	(0)
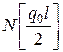
	-0.250 0.061 (0)	-0.874 -0.563 (-0.563)	-1.492 -1.250 (-1.25)	-2.500 -2.063 (-2.063)	- -2.937 (-3)

Рис 24. Изменение продольного перемещения по длине стержня (метод конечных разностей - вариант C)

Рис. 25. Изменение продольного усилия по длине стержня (метод конечных разностей - вариант C)

Дата добавления: 2014-01-20