Метод коллокаций

В методе коллокаций неизвестные параметры находятся из условия равенства нулю функции невязки в точках коллокации. После внесения аппроксимирующей функции (2.2.1) в дифференциальное уравнение упругого равновесия (5)

(2.5.1)

выбираются точки коллокации с координатами x_k и записывается система алгебраических уравнений

(2.5.2)

число которых равно, естественно, числу точек коллокации n. Внося полученные в процессе решения системы алгебраических уравнений u_i в соответствующую аппроксимирующую функцию, получаем выражение для перемещения. Выражение для усилия получаем на основе равенства (4). Разрабатывается программа для численной реализации полученных выражений, и производится счет при удержании необходимого числа точек коллокации, при этом производится сравнение приближенного решения с точным. Строятся графики в редакторе «Excel».

В случае варианта А запишем систему уравнений для двух точек коллокации:

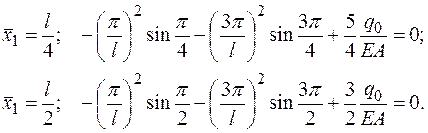(2.5.3)

Перепишем систему уравнений, раскрывая численные значения

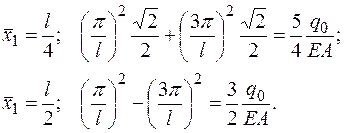(2.5.3)

Найдем определители системы

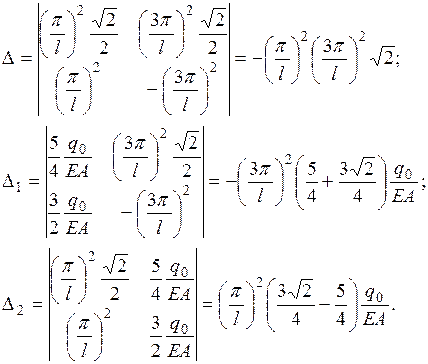(2.5.4)

Определим перемещения, приводя их к размерности точного решения,

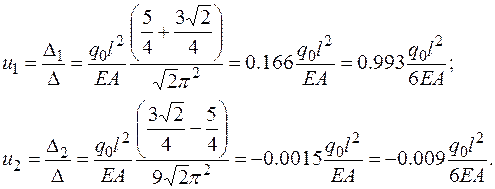(2.5.5)

Выражения для перемещения и усилия приобретают вид:

(2.5.5)

Результаты представим в таблице и на графиках (рис. 32, 33)

Таблица 12

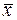
		0.25	0.5	0.75	1.0
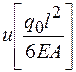
	(0)	0.709 (0.797)	1.002 (1.125)	0.709 (0.891)	(0)
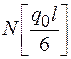
	3.148 (4)	2.186 (2.313)	(0.25)	-2.186 (-2.188)	-3.148 (-5)

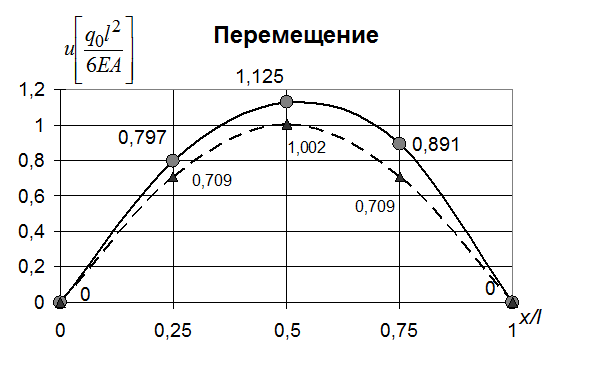
Рис 32. Изменение продольного перемещения по длине стержня (метод коллокаций - вариант А, 2 точки коллокации)

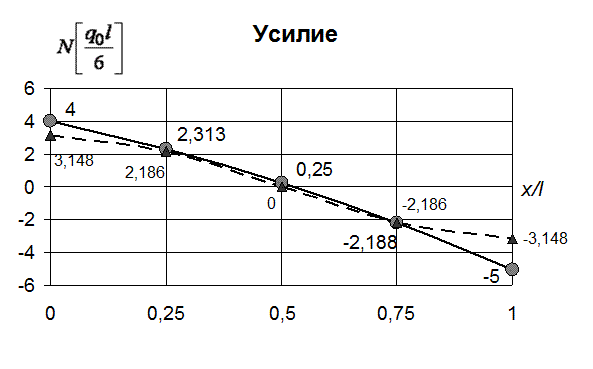
Рис. 33. Изменение продольного усилия по длине стержня (метод коллокаций - вариант А, 2 точки коллокации)

Для получения удовлетворительного решения необходимо брать большее число точек коллокации.

В случае варианта В запишем систему уравнений для двух точек коллокации:

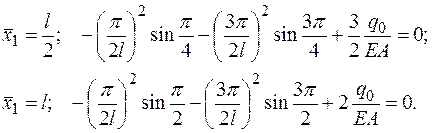(2.5.3)

Перепишем систему уравнений, раскрывая численные значения

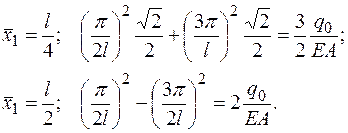(2.5.3)

Найдем определители системы

(2.5.4)

Определим перемещения, приводя их к размерности точного решения,

(2.5.5)

Выражения для перемещения и усилия приобретают вид:

(2.5.5)

Таблица 13

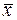
		0.25	0.5	0.75	1.0
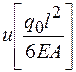
	(0)	1.903 (2.047)	3.531 (3.625)	4.636 (4.641)	5.027 (5)
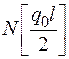
	2.598 (3.0)	2.414 (2.438)	1.872 (1.75)	1.027 (0.938)	(0)

Рис 34. Изменение продольного перемещения по длине стержня (метод коллокаций - вариант В, 2 точки коллокации)

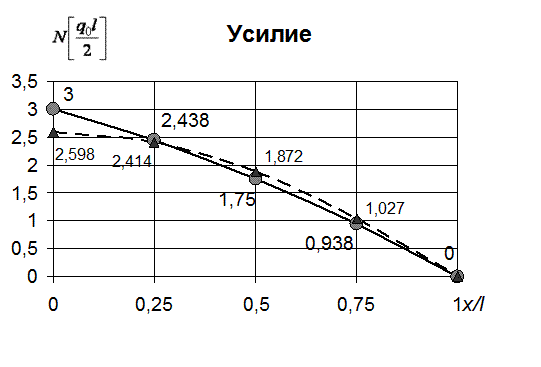
Рис. 35. Изменение продольного усилия по длине стержня (метод коллокаций - вариант В, 2 точки коллокации)

В случае варианта С запишем систему уравнений для двух точек коллокации:

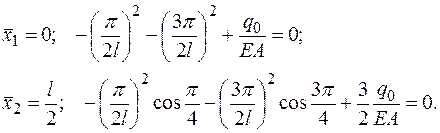(2.5.3)

Перепишем систему уравнений, раскрывая численные значения

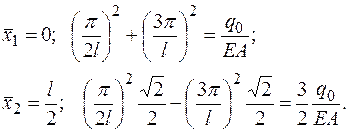(2.5.3)

Найдем определители системы

(2.5.4)

Определим перемещения, приводя их к размерности точного решения,

(2.5.5)

Выражения для перемещения и усилия приобретают вид:

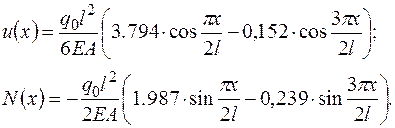(2.5.5)

Таблица 14

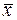
		0.25	0.5	0.75	1.0
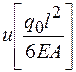
	3.642 (4)	3.447 (3.797)	2.790 (3.125)	1.592 (1.891)	(0)
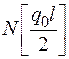
	(0)	-0.540 (-0.563)	-1.236 (-1.25)	-1.927 (-2.063)	-2.226 (-3)

Рис 36. Изменение продольного перемещения по длине стержня (метод коллокаций - вариант С, 2 точки коллокации)

Рис. 37. Изменение продольного усилия по длине стержня (метод коллокаций - вариант С, 2 точки коллокации)

Дата добавления: 2014-01-20