Введение. Математическое моделирование – могучее средство изучения природы, техники и человеческого общества

Математическое моделирование – могучее средство изучения природы, техники и человеческого общества. Что такое модель? Слово «модель» в переводе с итальянского означает «копия, образец, прототип». Изучив модель, мы познаем оригинал. Значит, математическая модель – это прототип какой-то части мира – объекта, системы, устройства, машины, процесса, прибора, изучая который, мы постигаем эту часть мира. Мы будем рассматривать математические модели в относительно узкой области – механике упругого тела.

При расчете напряженно-деформированного состояния инженерных сооружений приходится иметь дело не с самим сооружением, а с его расчетной моделью. Физическая модель сооружения (расчетная схема) получается путем принятия некоторых упрощающих гипотез, не оказывающих заметного влияния на реальное поведение сооружения. Математическая модель описывает поведение физической модели с помощью определенных соотношений, связывающих между собой параметры, определяющие такое поведение. В качестве параметров могут выступать геометрические размеры, жесткостные характеристики, деформации, перемещения, усилия, напряжения и т. п. Например, для определения перемещений и усилий от собственного веса Останкинской телебашни (рис. 1а) можно использовать очень простую физическую модель – прямолинейный стержень, подвергающийся действию переменной распределенной нагрузки (см. рис. 2).

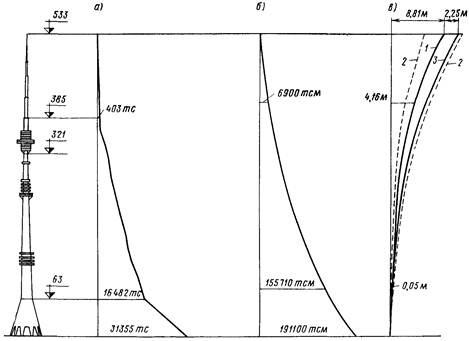
Рис. 1. Изменение продольных усилий от собственного веса (а), изгибающих моментов (б) и прогибов (в) от ветровой нагрузки по высоте Останкинской телебашни

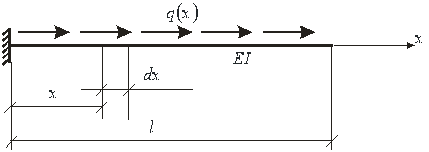
Рис. 2. Физическая модель (расчетная схема)

Математическая модель будет фигурировать в виде дифференциального уравнения

,

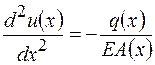включающего перемещение u(x), распределенную переменную по координате x нагрузку q(x) и продольную жесткость ЕА(x) (Е – модуль упругости материала, А(x) – площадь сечения). При этом продольное усилие N(x) и перемещение u(x) связаны между собой соотношением

.

Дата добавления: 2014-01-20