Геометрическая интерпретация ОЗЛП

Основная задача линейного программирования (ОЗЛП)

Рассмотрим основную задачу линейного программирования (ОЗЛП):

Найти неотрицательные значения переменных x₁, x₂, …, x_n, которые удовлетворяли бы условиям-равенствам

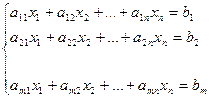
и обращали бы в максимум линейную функцию этих переменных:

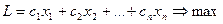
Любую задачу линейного программирования можно свести к стандартной форме: от минимума к максимуму можно перейти, изменив знак L на противоположный, а неравенства можно превратить в равенства путем введения новых неотрицательных переменных. Они будут входить в целевую функцию с нулевыми коэффициентами.

ПРИМЕР 2.4.

Студенту, чтобы получить зачет, необходимо набрать не менее 60 баллов. Ему предлагаются задания двух видов, минимальная оценка которых 6 и 12 баллов соответственно. Общее количество заданий 14. На каждое задание 1–ого вида он тратит в среднем 2часа, а 2-ого вида – 3 часа. Требуется минимизировать время сдачи зачета.

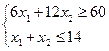
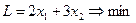
Введем дополнительные неотрицательные переменные x₃, x₄. Получим следующую систему ограничений:

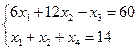
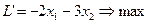
Назовем допустимым решением ОЗЛП неотрицательное решение x=(x₁, x₂, …, x_n), удовлетворяющее заданным условиям a. Множество допустимых решений назовем областью допустимых решений (ОДР). Оптимальным назовем решение x из допустимой области, которое обращает в максимум целевую функцию L.

Среди переменных, соответствующих элементам решения, различают базисные и свободные. Пусть m – число независимых уравнений в системе ограничений, n – число переменных. Тогда количество базисных переменных равно m, остальные переменные являются свободными r=n-m.

Пусть r=2 и свободными переменными являются x₁, x₂, тогда m уравнений можно записать в виде:

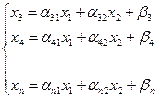
Построим на плоскости x₁Оx₂ прямые
x₃ =0, x₄ =0, … x_n =0. Так как все элементы допустимого решения должны быть неотрицательными, то для каждого элемента решения допустимой является только одна полуплоскость, в которой x_i >0. Часть первого координатного угла, принадлежащая одновременно всем этим полуплоскостям и есть ОДР.

Целевую функцию также выразим через свободные переменные.

Максимум этой функции достигается при тех же значениях переменных, что и максимум однородной функции (без свободного члена).

Построим на плоскости прямую 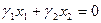Назовемее опорной прямой. Мысленно двигая эту прямую в сторону возрастания, заметим, что максимум достигается в одной из вершин ОДР, где по крайней мере 2 базисные переменные обращаются в нуль.

Если целевая функция в ОДР не ограничена сверху, то оптимального решения не существует. Если максимум достигается не в одной точке, а совпадает с границей ОДР, то существует бесконечное множество оптимальных решений.

ПРИМЕР 2.2. (условие в п.1)

Математическая модель:

х _i – количество ткани i -го вида (м)

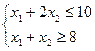
х_i ³0

L= х₁+х₂Þmax

{

{

х3 =10 - х1 -2х2 х4 = -8+ х1 + х2 L= х1+х2Þmax

х2 =5 –0.5 х1 х2 = 8- х1 опорная прямая: х2 = -х1

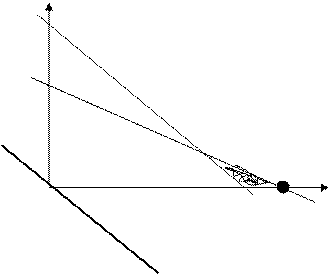
8 х₂

5 х₄ =0

х₃ =0

. 8 10

х₁

Ответ: х₂ =0; х₁ =10; L=10

Дата добавления: 2014-01-20