Анализ

1. Для получения максимальной прибыли фабрике следует выпускать только ткань 1-го вида количество 10м. Но тогда все лилипуты будут чем-то похоже друг на друга.

2. Можно повысить цену на ткань 2-го вида в 2раза. Тогда целевая функция будет иметь вид: L= х₁+2х₂ , а опорная прямая: х₂ = - 0.5х₁ В этом случае ОЗЛП будет иметь бесконечное множество оптимальных решений на отрезке.

3. Чтобы задача не имела оптимального решения, ОДР а) должна быть не ограничена сверху или б) не существовать вообще.

а) Область положительности х₃ должна быть направлена в ту же сторону, что и для х₄ Этого можно добиться, если не ограничивать сверху расход сырья.

б) Решений не будет существовать вообще, если прямые пересекутся ниже оси абсцисс. Например, ограничение на суточный расход станет ниже 8ед. или суточный спрос на ткань превысит 10м

ПРИМЕР 2.4. (условие в п.2)

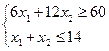
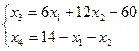
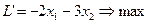Опорная прямая:

14

5

10 14

Ответ: х₁=0; х₂=5; L’=-15; L=15

ЗАМЕЧАНИЯ.

1. Если система ограничений задачи линейного программирования содержит всего 2 переменные, то область допустимых решений можно найти, решив систему неравенств.

2. Построить опорную прямую можно, опираясь на то, что она перпендикулярна вектору нормали.

ПРИМЕР 2.5. Магазин закупает печенье 2-х сортов по цене с_i за 1 кг i-ого вида и получает прибыль p_i от его реализации. Денежный ресурс ограничен А. Спрос покупатель не превышает В. Максимизировать прибыль при условии полного удовлетворения спроса.

	цена	прибыль	количество
1 сорт			х1
2 сорт			х2
Условия	≤ 600	max	≥ 50

ПРИМЕЧАНИЯ. 1. Для построения ОДР можно не добавлять дополнительные переменные. Достаточно просто решить систему неравенств. 2. Опорную прямую можно строить с помощью вектора нормали. Координатами вектора нормали являются коэффициенты при переменных в целевой функции. Вектор нормали показывает направление возрастания целевой функции. Опорная прямая проводится перпендикулярно вектору нормали. В примере N=(3,1)

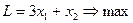
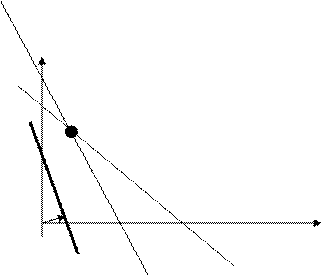
60

30 50

Дата добавления: 2014-01-20