Анализ. 1. Следует покупать печенье обоих сортов, т.к

1. Следует покупать печенье обоих сортов, т.к. покупка только 1 сорта (наиболее прибыльного) не удовлетворяет спрос населения.

Оптимальное решение достигается в точке пересечения двух прямых. Найдем эту точку, решив систему уравнений:

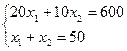
х₁=10; х₂=40; L=70

2. Бесконечного множества решений можно достигнуть, повысив цену реализации на 2 сорт или понизив цену на 1 сорт так, чтобы прибыль от продажи была пропорциональна закупочной цене.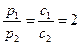

3. Решения не будет существовать (ОДР – пустое множество), если спрос покупателя увеличится и станет более 60.

4. Если закупочная сумма неограниченна, то оптимального решения не будет

(ОДР не ограничена сверху)

Задание 2.1. Рассмотрим пример 2.5. со следующими данными.

	цена	прибыль	количество
1 сорт			х1
2 сорт			х2
Условия	≤ 1000	max	≥ 5 0

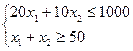
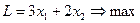
ОТВЕТ: х₁=5;0 х₂=0; L=15

ПРАВИЛО. Оптимальное решение ОЗЛП (если оно существует) достигается при такой совокупности значений переменных x₁, x₂, …, x_n ,, где по крайней мере k=n-m из них обращаются в нуль, а остальные неотрицательны.

Отсюда вытекает идея метода «последовательных проб».

а) выбираем k свободных переменных и полагаем их равными 0;

б) вычисляем значения базисных переменных при нулевых значениях сводных.

Если все они оказались неотрицательными, значит мы нашли допустимое (необязательно оптимальное) решение.

Для простых задач, где число переменных невелико, «слепой перебор» может привести к оптимальному решению довольно быстро.

ПРИМЕР 2.4.

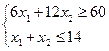
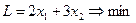
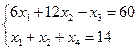
№	x1	x2	x3	x4	L
			-60		Решение не допустимое
		-4			Решение не допустимое

ПРИМЕР 2.5.

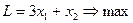
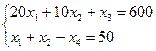
№	X1	x2	x3	x4	L
				-50	Решение не допустимое
			-400		Решение не допустимое
				-20	Решение не допустимое

Но в практических задачах число переменных очень велико, порядка сотен. Для таких задач простой перебор становится невозможным. Например, при n= 30, m =10 число переборов свободных переменных свыше 30 миллионов!

Дата добавления: 2014-01-20