Элементы теории графов

Транспортная задача.

Двойственные задачи линейного программирования.

ПРЯМАЯ	ДВОЙСТВЕННАЯ
Система ограничений: Ах=B xi ≥0 Целевая функция: L=Cx → max	Система ограничений: A^Tu=C^T ui ≥0 Целевая функция: L=B^Tu → min

Существуют частные типы задач линейного программирования, которые в силу особой своей структуры, допускают решение более простыми методами. Например, транспортная задача. Она ставится следующим образом: имеются n пунктов отправления (ПО) A₁, A₂,… A_n-1, A_n, в которых сосредоточены запасы каких-то однородных грузов в количестве a₁, a₂,… a_n-1, a_n единиц. Имеются m пунктов назначения (ПН) B₁, B₂,… B_n-1, B_n, подавших заявки соответственно на b₁, b₂,… b_n-1, b_n единиц груза. Сумма всех заявок равна сумме всех запасов.

Известны стоимости перевозки единицы груза от каждого пункта отправления до каждого пункта назначения. Представим их в виде прямоугольной матрицы:

Считается, что стоимость перевозки нескольких единиц груза пропорциональна их числу.

Требуется составить такой план перевозок (откуда, куда и сколько единиц везти), чтобы все заявки были выполнены, а общая стоимость всех перевозок минимальна.

Обозначим x_ij -количество единиц груза, отправляемого из A_i в B_j Совокупность (x_ij) будем называть «планом перевозок» или решением, а сами величины «перевозками».

Составим ОЗЛП.

1. Суммарное количество груза, направляемого из каждого ПО во все ПН, должно быть равно запасу груза в данном пункте:

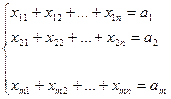
2. Суммарное количество груза, доставляемого в каждый ПН из всех ПО, должно быть равно заявке, поданной данным пунктом:

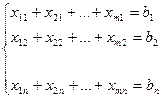
3. Суммарная стоимость всех перевозок должна быть минимальной:

То, что все коэффициенты в условиях-равенствах равны 1, позволяет решать задачу очень простыми способами.

Число линейно-независимых уравнений = m+n-1, общее число переменных = mn, число базисных переменных = m+n-1, а число свободных k=mn-(m+n-1)=(m-1)(n-1)

Так как оптимальное решение достигается в одной из вершин ОДР, то по крайней мере k перевозок должны быть равны нулю. Допустимый план будем называть опорным, если в нем отличны от нуля не более m+n-1 базисных перевозок.

Представим транспортную задачу в виде некоторой таблицы, называемой транспортной.

	B1	B2	…	Bn
A1	c11	c12	…	c1n	a1
A2	c21	c22	…	c2n	a2
…	…	…	…	…	…
Am	cm1	cm2	…	cmn	am
	b1	b2	…	bn

МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА

Построение начального плана согласно этому методу начинается с верхнего угла транспортной таблицы. Распределение груза первого поставщика происходит таким образом, что сначала максимально удовлетворяются заявки первого потребителя, затем второго и т.д. до полного распределения груза, имеющегося в A₁ Затем подобным же образом распределяется груз второго поставщика и т.д.

ПРИМЕР 2.6.

	B1	B2	B3	B4	ai	остаток
A1	1 3	3 5	7 2	1	10	7 2 0
A2	2	4	2 8	3 7	15	7 0
A3	6	5	4	1 7	7	0
bj	3	5	10	14	32
	0	0	8 0	7 0

Действуя описанным способом, мы получаем ступенчатую фигуру. В процессе решения получили 6 базисных клеток. Так как m+n-1= 3+4-1=6, то план невырожденный. Его можно принять за опорный.

Так как на стоимость перевозок в этом методе не обращается внимание, то полученный опорный план, вероятно, далек от оптимального.

МЕТОД МИНИМАЛЬНОГО ЭЛЕМЕНТА.

Распределение груза в этом методе начинается с одной из вершин минимальной стоимости. Также при каждом распределении необходимо максимально удовлетворить заявки выбранного потребителя. Очередное распределение выбирается из условия минимальной стоимости перевозок.

ПРИМЕР 2.7.

	B1	B2	B3	B4	ai	остаток
A1	1	3	7	1 10	10	0
A2	2 3	4 5	2 7	3	15	8 5 0
A3	6	5	4 3	1 4	7	3 0
bj	3	5	10	14	32
остаток	0	0	7 0	4 0

Чтобы улучшить решение, следует перейти к другому плану. Самый простой способ – метод Жордана-Гаусса. Он заключается в целенаправленном переборе планов. Какую клетку выбрать, чтобы переход к новому решению привел к уменьшению значения целевой функции?

Рассмотрим произвольную свободную клетку. Однозначным образом можно выбрать замкнутую цепочку, называемую циклом, состоящую из вертикальных и горизонтальных звеньев, одной из вершин которой является выбранная свободная клетка, а остальными вершинами – занятые клетки. Начиная со свободной клетки (она – первая), пометим все нечетные вершины знаком «+», а четные - знаком «-». Переброской перевозок по циклу назовем увеличение перевозок в положительных вершинах и уменьшение в отрицательных. Перебросить по циклу можно не более чем минимум в отрицательных вершинах цикла.

ПРИМЕР 2.6.

Выберем в рассмотренном выше примере свободную клетку (3,2). Определим замкнутый цикл, последовательно расставляя знаки «+» и «-».

	B1	B2	B3	B4	ai
A1	1 3	3 - 5	7 + 2	1	10
A2	2	4	2 - 8	3 + 7	15
A3	6	5 +	4	1 - 7	7
bj	3	5	10	14	32

Минимумом в отрицательных вершинах является число 5. Его и занесем в клетку (3,2). Далее пройдем по всему циклу, меняя значения перевозок. Получим новый базисный план:

	B1	B2	B3	B4	ai
A1	1 3	3	7 7	1	10
A2	2	4	2 3	3 12	15
A3	6	5 5	4	1 2	7
bj	3	5	10	14	32

Ценой цикла будем считать разность между суммой стоимостей перевозок в положительных вершинах цикла и суммой перевозок в отрицательных вершинах. Если цена цикла < 0, то выгодно перебросить перевозки по этому циклу. Суммарные перевозки при этом не изменятся. Цена цикла говорит, на сколько изменится суммарная стоимость перевозок при переброске по циклу 1 единицы груза. Например, в рассмотренном примере цена цикла d₃₂=7+3+5-(1+2+3)=9>0. Следовательно, переброска 1 единицы груза по этому циклу приводит к увеличению суммарной стоимости перевозок на 9. В примере по циклу было переброшено 5 единиц, следовательно, затраты на перевозки увеличились на 45.

МЕТОД ЖОРДАНА-ГАУССА.

Метод заключается в переборе дешевых клеток и просчете цены их цикла. Если цена отрицательна, то следует перебросить по этому циклу столько единиц груза, сколько возможно (минимум в отрицательных вершинах). Если существует несколько свободных клеток с отрицательной ценой цикла, то лучше выбрать ту, для которой она максимальна по модулю. Когда не останется ни одной свободной клетки с отрицательной ценой цикла, тогда найденный план является оптимальным.

	B1	B2	B3	B4
A1	1 3	3 5	- 7 2	+ 1
A2	2	4	2 8 +	3 7 -
A3	6	5	4	1 7

d₂₁=2-1+7-2=6>0

d₃₁=6-1+7-2+3-1=12>0

d₂₂=4-3+7-2=4>0

d₃₂=9>0

d₃₃=4-2+3-1=4>0

d₁₄=1-3+2-7=- 4<0

Следовательно, выгодным является только цикл клетки (1,4). По нему можно перебросить min(2,7) =2 единицы груза. Получим следующий план.

	B1	B2	B3	B4
A1	1 3 -	3 5	7	1 2 +
A2	+ 2	4	2 10	3 5 -
A3	6	5	4	1 7

d₂₁=2-1+1-3=-1<0

d₂₂=4-3+1-3=-1<0

Для всех остальных циклов цена >0

Выберем клетку (2,1)

min(3,5) =3

	B1	B2	B3	B4
A1	1	3 5	7	1 5
A2	2 3	4	2 10	3 2
A3	6	5	4	1 7

d₂₂=4-3+1-3=-1<0

Для всех остальных циклов цена >0

min(2,5) =2

	B1	B2	B3	B4
A1	1	3 3	7	1 7
A2	2 3	4 2	2 10	3
A3	6	5	4	1 7

Для всех циклов цена >0, следовательно план оптимальный

Ответ: x₁₂=3; x₁₄=7; x₂₁=3; x₂₃=10; x₂₂=2; x₃₄=7; L=3∙3+7∙1+3∙2+10∙2+2∙4+7∙1=57

МЕТОД ПОТЕНЦИАЛОВ.

Обозначим переменные задачи, двойственной к транспортной через - u_i и v_j Их называют потенциалами пунктов отправления и пунктов назначения соответственно.

Двойственная задача заключается в нахождении потенциалов u_i и v_j, удовлетворяющих ограничениям v_j - u_i ≤ с _ij и максимизирующих функцию цели

КРИТЕРИЙ ОПТИМАЛЬНОСТИ. Для того чтобы план перевозок в транспортной задаче был оптимален, необходимо и достаточно, чтобы нашлись потенциалы u_i (пункта отправления) и v_j (пункта назначения) такие, что:

v_j - u_i = с _ij , если х_ij>0

v_j - u_i ≤ с _ij , если х_ij=0

ЭКОНОМИЧЕСКИЙ СМЫСЛ: v_j можно рассматривать как цену груза в ПН, u_i – цену груза в ПО. Тогда оптимальным будет план, в котором перевозки осуществляются по путям, где разность цен равна цене перевозки единицы груза.

Алгоритм.

1. Выберем любой базисный план.

2. Составим систему уравнений v_j - u_i = с _ij для базисных переменных

3. Так как система содержит m+n-1 уравнение и m+n неизвестных, то одну из них можно задать произвольно (например, =0). После этого определим остальные потенциалы.

4. Для каждой из свободных клеток вычислим величины a_ij=v_j-u_i

5. Если все a_ij≤ с_ij то план оптимален. Задача решена.

6. В противном случае рассмотрим все клетки, для которых a_ij> с_ij. Выберем свободную клетку, для которой реализуется max(a_ij-c_ij), введем ее в базис, образуем цикл и построим новое базисное решение. Переходим к п.2

ПРИМЕР 2.7.

	B1	B2	B3	B4
A1	1 3	3 5	7 2	1
A2	2	4	2 8	3 7
A3	6	5	4	1 7

Составим разность потенциалов для базисных клеток:

v₁-u₁=1

v₂-u₁=3

v₃-u₁=7

v₃-u₂=2

v₄-u₂=3

v₄-u₃=1

Положим u₁=0 и найдем остальные потенциалы

	B1	B2	B3	B4	ui
A1	1 3	3 5	7 2	8) 1	0
A2	-4) 2	-2) 4	2 8	3 7	5
A3	-6) 6	-4) 5	0 4	1 7	7
vj	1	3	7	8

a₁₄> с₁₄, следовательно построим цикл для клетки (1,4) и перебросим по нему максимально возможные перевозки.

	B1	B2	B3	B4	ui
A1	1 3 -	3 5	0) 7	1 2 +	0
A2	3) + 2	5) 4	2 10	3 5 -	-2
A3	1) 6	3) 5	0) 4	1 7	0
vj	1	3	0	1

a₂₁> с₂₁

a₂₂> с₂₂

Выберем клетку (2,1)

min(3,5) =3

	B1	B2	B3	B4	ui
A1	0) 1	3 5	0) 7	1 5	0
A2	2 3	5) 4	2 10	3 2	-2
A3	0) 6	3) 5	0) 4	1 7	0
vj	0	3	0	1

a₂₂> с₂₂

min(2,5) =2

	B1	B2	B3	B4	ui
A1	1) 1	3 3	1) 7	1 7	0
A2	2 3	4 2	2 10	2) 3	-1
A3	1) 6	3) 5	1) 4	1 7	0
vj	1	3	1	1

Для всех клеток a_ij≤ с_ij , следовательно план оптимальный

Ответ: x₁₂=3; x₁₄=7; x₂₁=3; x₂₃=10; x₂₂=2; x₃₄=7; L=3∙3+7∙1+3∙2+10∙2+2∙4+7∙1=57

ПРИМЕЧАНИЕ. Если условие равенства запасов груза в ПО и суммарной потребности в грузе ПН нарушено, то

1) если всех заявок удовлетворить нельзя, то вводится фиктивный ПО А_m+1, стоимости перевозок из которого равны 0;

2) если существует избыток груза, то вводится фиктивный ПН B_n+1, стоимости перевозок в который равны 0.

Раздел III. ГРАФОВЫЕ МОДЕЛИ.

G: d→[i,j]

Неориентированным графом называется тройка (I,D,G), в которой I – множество вершин, D – множество ребер и G – отображение, которое каждому ребру ставит в соответствие неупорядоченную пару вершин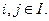

Если каждому ребру соответствует упорядоченная пара вершин 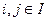, то граф называется ориентированным графом , а ребро называется дугой и обозначается (i,j).

ПРИМЕР 3.1.

а) неориентированный граф б) ориентированный граф

Путь – это упорядоченная последовательность дуг, начало каждой из которых совпадает с концом предыдущей. Контур – путь, у которого начальная вершина совпадает с конечной. Для неориентированного графа аналогом понятия путь является – цепь, а контура - цикл.

Простой цикл – цикл, в котором любая пара вершин соединена не более чем одним ребром. Гамильтонов цикл – простой цикл, проходящий через все вершины графа.

ПРИМЕР 3.2.

а) неориентированный граф б) варианты Гамильтонова цикла

Связный граф – граф, у которого любая пара вершин может быть соединена цепью (для неориентированного графа) или путем (для ориентированного графа)

Дерево – неориентированный граф без циклов.

Остов графа – подграф неориентированного графа, являющийся деревом.

ПРИМЕР 3.3. Для предложенного графа существует 31 вариант остовов.

а) граф б) варианты остова

Если каждой вершине сопоставить число, то оно будет называться интенсивностью вершины. Если на множестве дуг задать числовую функцию, то каждое ребро приобретет вес.

ПРИМЕР 3.4. Автомобилисту необходимо проехать из п.А в п.В.

10 0

А 7 В

4 2

Ориентированный связный граф, вершинам которого сопоставлены числа (интенсивности, пропускные способности) или дугам которого сопоставлены числа (стоимости, протяженности, пропускные способности), принято называть сетью.

Потоком на сети называется совокупность величин, заданных на множестве дуг, { x_d }:

,

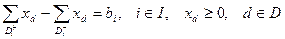где – множество дуг, исходящих из вершины i, а 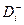– множество дуг, входящих в нее;
b_i – интенсивность вершины i.

Величина x_d называется значением потока по дуге d и интерпретируется как количество продукта, пропускаемое по данной дуге

Сеть с заданными пропускными способностями дуг будем считать реальной, если в ней каждой выходящей дуге сопоставлено число, не превышающее суммарную пропускную способность всех входящих в соответствующую вершину дуг.

ЗАДАЧИ ОПТИМИЗАЦИИ НА СЕТИ.

1. Об оптимальном распределении грузопотоков на сети (транспортная задача)

2. О кратчайшем пути между двумя пунктами (вершинами.)

3. О совокупности дорог, соединяющих пункт отправления со всеми пунктами назначения (минимальный остов)

4. Об оптимальном пути для коммивояжера (оптимальный Гамильтонов цикл)

5. О максимальном потоке на сети.

Дата добавления: 2014-01-20