Кратчайший путь в ориентированном графе

Задача о кратчайшем пути.

ЗАДАЧА. Задан неориентированный граф. Функция стоимости - c_ij. Найти оптимальный путь между двумя вершинами.

АЛГОРИТМ МИНТИ.

1. Введем переменную c^/_ij =c_ij в начальный момент.

2. Пометим начальную вершину числом m₀=0.

3. Для каждой помеченной вершины i будем метить те вершины, которые можно достичь из I по дугам с нулевым значением, т.е. m_j=i еще не помеченные вершины j для которых c^/_ij=0. Пометки расставляем до тех пор, 1) пока не пометим конечную вершину пути или 2) пока нельзя будет сделать дальнейшие пометки.
В случае 1) искомый путь (определяется по пометкам) найден и задача решена.

4. Для всех помеченных вершин I определим

5. Уменьшим c^/_ij при 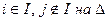и перейдем к п.3

ПРИМЕР 3.5.

М 9 К

2 2 4 3

А 3 1 2 7 В

Р 5 Т

Пометим вершину А числом m_A= 0. Так как дальнейшая пометка невозможна, переходим к п.4: Δ=2, c^/_АМ=0, c^/_АР=1

Пометим вершину М: m_М= А. Δ=1, c^/_МР=0, c^/_АР=0, c^/_МТ=1, c^/_МК=8

Пометим вершину Р: m_Р= А. Δ=2, c^/_РК=3, c^/_РТ=4, c^/_МТ=0, c^/_МК=7

Пометим вершину Т: m_Т=М. Δ=2, c^/_ТВ=5, c^/_ТК=0

Пометим вершину К: m_К=Т. Δ=3, c^/_КВ=0

Пометим вершину В: m_В=К

Получили оптимальный путь: A→M→T→K→В. Длина пути=11

МЕТОД расстановки пометок.

ДАНО: (I,D,G) – неориентированный граф;

L(i,j) – длина ребра [i,j];

n, k – начальная и конечная вершины цепи.

НАЙТИ: min L(n, k)

АЛГОРИТМ

1. Пометим каждую вершину индексом λ_i
2. Примем λ_k =0; все остальные λ_i =∞
3. Найдем ребро (i,j), для которого λ_j –λ_i >L(i,j) и заменим λ_j =λ _j +L(i,j)
4. Продолжим процесс до тех пор, пока существует хотя бы одно ребро, для которого можно уменьшить λ_j
5. Найдем путь движением от начальной вершины к конечной по убыванию индексов переходом по дугам, для которых λ_i –λ_j =L(i,j)

4 В   2 3 А  

ПРИМЕР 3.6. Найти кратчайший путь от А до В.

3 4 2

5 2 2

5 2

3 3 4 3

2 4 1

РЕШЕНИЕ

Обозначим Г(х) – множество конечных вершин дуг исходящих из x, а Г^-1(х) – множество начальных вершин дуг, входящих в х.

Порядковой функцией О(х) назовем функцию, определенную на множестве вершин: если x_j Є Г(x_i), то O(x_j)>O(x_i), т.е. если вершина x_j следует за вершиной x_i, то значение порядковой функции в ней больше, чем в x_i Величину O(x_i) будем называть уровнем вершины x_i.

ЗАДАЧА. Задан ориентированный граф G=(X,U) без циклов и числовая функция на дугах. Построить минимальный путь из вершины А в вершину В.

ТЕОРЕМА ОПТИМАЛЬНОСТИ. Если некоторый путь, соединяющий вершины x_i и x_j, является минимальным, то его подпуть также является минимальным.

АЛГОРИТМ БЕЛЛМАНА.

1. Построим порядковую функцию О(х), полагая О(А)=0.

2. Начиная с вершины В, рассматриваем последовательно все вершины графа в порядке убывания его порядковой функции и приписываем каждой вершине число, равное минимальному значению пути от этой вершины до В.

ПРИМЕР 3.7.

М 9 К

2 2 4 3

А 1 2 В

3 7

Р 5 Т

1. О(А)=0, О(М)=1, О(Р)=2, О(К)=3, О(Т)=4, О(В)=5

2. S(T)=7, S(K)=min(9,3)=3, S(P)=min(7,12)=7, S(M)=min(12,9,8)=8, S(A)=min(10,10)=10

Минимальный путь А→Р→К→В

АЛГОРИТМ ФОРДА.

1. Положим λ_i=∞ в каждой вершине, кроме λ₀=0

2. Ищем дугу (x_i, x_j ): λ_j -λ_i >l(x_i, x_j ) и заменяем λ_j на λ_i+l(x_i, x_j ) <λ_j
Поступаем так до тех пор, пока возможно найти дугу, уменьшающую хотя бы одно значение.

ПРИМЕР 3.8.

М 9 К

2 2 4 3

А 1 2

3 1 7 В

Р 5 Т

λ_А =0, λ_Р =3 λ_М =2,λ_К=7, λ_Т=8, λ_В=10

ПРИЛОЖЕНИЕ ЗАДАЧИ.

1. Планирование транспортных маршрутов

2. Прокладка магистрали между двумя объектами

3. Установление последовательности взаимосвязанных работ

Дата добавления: 2014-01-20