
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение усилия процесса вытяжки
|
|
|
|
Усилие процесса вытяжки определяется из условия равенства внешнего и внутреннего усилия сопротивления.
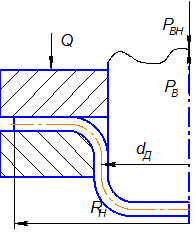

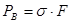
Сила и напряжение – векторные величины. Возьмем напряжения в той части заготовки, в которой направление напряжений совпадает с направлением усилия сопротивления и противоположно внешнему, то есть цилиндрический участок заготовки, а напряжение – меридиональное, действующее вдоль образующей ( ).
).
 ,
,
где  ,
,  .
.
Найдем напряжение в цилиндрической части, используя принцип суперпозиций (наложение одного фактора на другой путем их суммирования). Напряжение в цилиндрической части будем определять как сумму напряжений от нескольких факторов, причем эти составляющие препятствуют, оказывают сопротивление.
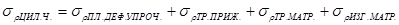
В данном случае нас интересует максимальное усилие.
На процесс формирования усилия в начальной стадии оказывает влияние и угол, под которым располагается свободный участок
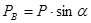

Определим каждое из слагаемых:
§  (если
(если  , то получаем не вытяжку, а вырубку)
, то получаем не вытяжку, а вырубку)
§ 
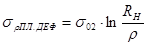 - для идеального случая.
- для идеального случая.
Чтобы учесть упрочнение, мы принимаем модель, в соответствии с которой элементы фланца заготовки упрочняются одинаково, причем также как кромка заготовки. Чтобы учесть упрочнение введем степенную функцию, которая учитывает упрочнение: 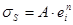 , где
, где  - константы механических свойств
- константы механических свойств
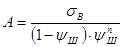 ,
, 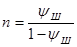 .
.
Интенсивность деформаций заменим максимальной величиной, для кромки ей является тангенциальная деформация
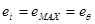 ,
,
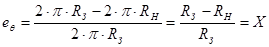 .
.
Тангенциальная деформация кромки равна относительной величине перемещения 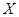 . Таким образом
. Таким образом 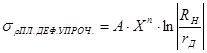 , при
, при 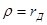 (
( - радиус детали)
- радиус детали)
 ,
,
где  - коэффициент вытяжки,
- коэффициент вытяжки, 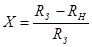 - перемещении кромки, соответствующее максимальному усилию.
- перемещении кромки, соответствующее максимальному усилию.
Последнее выражение получили в результате разложения в степенной ряд 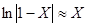 , так как
, так как 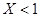 .
.
Тогда  .
.
Это выражение позволяет определить, при каких величинах перемещения 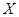 кромки
кромки 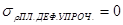 .
.
При 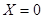 и
и 
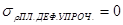 .
.
То есть значение 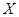 , при котором напряжение достигает экстремума. Это выражение позволяет учитывать размеры фланца с одной стороны и упрочнение – с другой стороны.
, при котором напряжение достигает экстремума. Это выражение позволяет учитывать размеры фланца с одной стороны и упрочнение – с другой стороны.
Чтобы найти экстремум нужно продифференцировать полученное выражение по 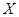 .
.
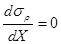
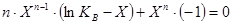
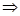
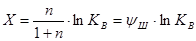
§ Найдем составляющую трения заготовки на поверхности прижима и матрицы. Будем считать, что прижим является абсолютно жестким, поэтому усилие прижима приходится на площадь поверхности торца.

 ,
,
где 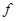 - коэффициент трения,
- коэффициент трения,  - давление прижима на заготовку
- давление прижима на заготовку
 .
.
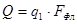 ,
,
 находится по табличным данным,
находится по табличным данным,
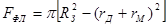 ,
,
 - радиус матрицы,
- радиус матрицы,
 - условное давление [МПа], которое прикладывается по всей поверхности фланца в начале процесса вытяжки,
- условное давление [МПа], которое прикладывается по всей поверхности фланца в начале процесса вытяжки,
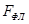 - площадь фланца, находящаяся под прижимом,
- площадь фланца, находящаяся под прижимом,
 можно найти теоретически из условия
можно найти теоретически из условия
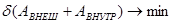 ,
,
то есть вариация работ от внешних и внутренних сил на возможных перемещениях минимальна.
Вариация – это возможное перемещение.

Внутренние силы – это силы, связанные с напряжениями, возникающими внутри заготовки.  - это напряжение внешних сил.
- это напряжение внешних сил.
 .
.
Задача решается путем решения интегральных уравнений, которые представляются в виде системы, и в них нужно найти те параметры процесса, по которым минимизируется вариационное выражение.
В данном случае 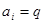 . Причем в границах интегрирования
. Причем в границах интегрирования 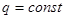 .
.
Давление  должно быть оптимальным, а именно таким, чтобы усилие вытяжки было при нем наименьшим при достаточном качестве изделия.
должно быть оптимальным, а именно таким, чтобы усилие вытяжки было при нем наименьшим при достаточном качестве изделия.
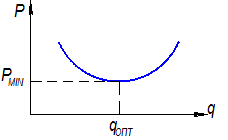
Большое давление  приводит к росту трения под прижимом и росту напряжений в опасном сечении.
приводит к росту трения под прижимом и росту напряжений в опасном сечении.
Малое значение  приводит к небольшому гофрообразованию фланца, которое необходимо устранить, применяя дополнительное напряжение в опасном сечении.
приводит к небольшому гофрообразованию фланца, которое необходимо устранить, применяя дополнительное напряжение в опасном сечении.
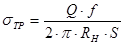 .
.
Кроме того, что на ребре матрицы происходит изгиб, происходит еще и трение
Составим схему действия сил на бесконечно малый элемент при изгибе тонкой нити. Уравнение действия сил называют уравнением Эйлера.
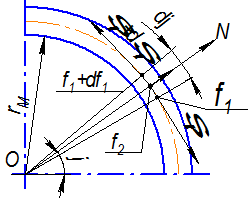
Составим уравнение равновесия сил на ось ОN
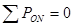 .
.
Пренебрегая слагаемыми более высокого порядка, мы получаем тождество


Составим уравнение равновесия сил на ось, перпендикулярную ОN
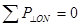
 ,
,
Учтем, что  ,
, 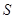 - толщина,
- толщина, 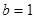 - ширина,
- ширина,  , так как
, так как 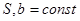 ,
,
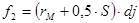 ,
,
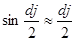 ,
,
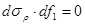
после преобразований получим уравнение Эйлера:
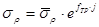 ,
,
где  .
.
Чем больше угол закручивания, тем труднее перетащить гибкую нить.
Таким образом, получаем окончательное напряжение в опасном сечении в цилиндрической части
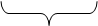


Данное уравнение используется в том случае, если при вытяжке используется ненормализованные технологические параметры, то есть отличные от справочных.
Например:
1. Вытяжка заготовки с узким фланцем и маленьким радиусом закругления.
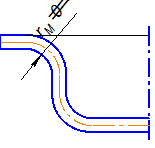
2. Когда требуется большое усилие прижима, например, при вытяжке тонкостенных заготовок с большим фланцем.
Коэффициент вытяжки для тонких заготовок меньше, чем для толстых

Таким образом, 
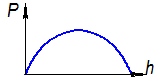
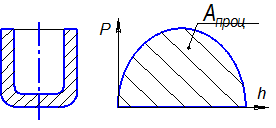
Для кривошипных прессов важным показателем является работа процесса.
Геометрически работа процесса определяется площадью фигуры, находящейся под графиком усилия процесса.
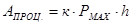 ,
,
где 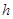 - высота детали,
- высота детали,  .
.
Цилиндрическая деталь  Деталь с фланцем
Деталь с фланцем 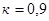

|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 546; Нарушение авторских прав?; Мы поможем в написании вашей работы!