Оптимальная фильтрация. Согласованный фильтр

ЛЕКЦИЯ №26

Рассматриваем ДКС.

Допустим: 0 – 10111,

1 – 01000.

Эти комбинации будут иметь различные спектры.

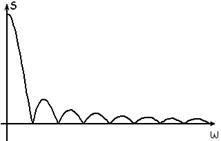
Если на приёме поставим фильтр, АЧХ которого в точности повторяет спектр S(ω), то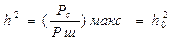

Учитывая, что в канале связи есть помеха,

Спектр Z(ω) получится:

Получим максимальное отношение сигнал/шум.

Известно, что любой сигнал соответствует определённому спектру. Спектр показывает распределение мощности сигнала по частоте.

Допустим имеем модель ДКС.

Пусть S₁(t) и S₂(t) – различные кодовые комбинации длиной n S₁(t) и S₂(t).

Можно утверждать, что S₁(ω)≠ S₂(ω), т.к. S₁(t)≠S₂(t), поскольку существует взаимно-однозначное соответствие между сигналом и спектром его мощности.

Для переданного сигнала S₁(t) можно утверждать: Z(ω)=S₁(ω)+ξ(ω).

В результате, если в точке приёма будут использоваться фильтры, АЧХ которых с точность до коэффициента а повторяют спектры S₁(ω) и S₂(ω), то на выходе СФ (согласованного фильтра)

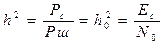
Результат сходен с результатом, который получается при использовании приёмника Котельникова. Поэтому согласованную фильтрацию часто называют оптимальной.

Если АЧХ фильтра не в полном объёме повторяет спектр передаваемого сигнала, фильтр называют квазиоптимальным.

Достоинства оптимальной фильтрации по сравнению с приёмником Котельникова.

1) Нет необходимости синфазности эталонного и принятого сигнала.

2) Согласованный фильтр сравнивает эталонный и принятый сигналы в частотной области.

Недостаток:

С увеличением длины кодовой комбинации увеличивается h₀², но увеличивается время задержки принятия решения. Это есть ограничение по променению метода в соответствующих физических средах.

Таким образом,

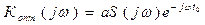
a < 1, если СФ состоит из неактивных элементов.

а ≥ 1, если СФ состоит из активных элементов.

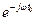– учитывает задержку t₀

S(jω) – спектр сигнала.

К_опт – коэффициент передачи с учётом задержки.

Учитывая, ч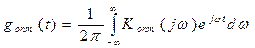то

, то ,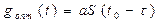

а сигнал на выходе

Т.о. сигнал на выходе СФ – автокорреляционная функция.

Пример.

Пусть: S_вх(t) = 1-111-1

Определить: S_вых(t) –?

Решение:

1) τ₀=0∙τ_э

S_вх(t)= 1-111-1

S_вх(t+τ₀)= 1-111-1

1 111 1 B(0∙τ_э) = 5

2) τ₀=1∙τ_э

S_вх(t)= 1-1 11-1

S_вх(t+τ₀)= 1-11 1-1

-1-11-1 B(1∙τ_э) = – 2

3) τ₀=2∙τ_э

S_вх(t)= 1-1 1 1-1

S_вх(t+τ₀)= 1-1 1 1-1

1-1-1 B(2∙τ_э) = – 1

4) τ₀=3∙τ_э

S_вх(t)= 1-1 1 1-1

S_вх(t+τ₀)= 1-1 1 1-1

1 1 B(3∙τ_э) = 2

5) τ₀=4∙τ_э

S_вх(t)= 1-1 1 1-1

S_вх(t+τ₀)= 1-1 1 1-1

-1 B(4∙τ_э) = – 1

6) τ₀=5∙τ_э

S_вх(t)= 1-1 1 1-1

S_вх(t+τ₀)= 1-1 1 1-1

0 B(5∙τ_э) = 0

Сдвигая влево, убеждаемся, что полученная функция симметрична относительно оси ординат. Сдвиг в – τ даёт зеркальное отображение.

Получили сигнал вида:

Дата добавления: 2014-01-20