
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 1. Языки первого порядка
|
|
|
|
Языки первого порядка.
Высказывания и высказывательные формы.
Математические суждения мы обычно записываем в виде текстов на русском языке, обогащенном математической символикой. Предложения, выражающие определенные суждения, называются высказываниями. Они характеризуются тем, что могут быть истинными или ложными, и этим отличаются от повелительных или вопросительных предложений.
Например, 2x2 = 4, «Рим — столица Франции» суть высказывания, а предложения «Который час?» или «Решить квадратное уравнение х2 + Зх — 2 = 0» высказываниями не являются.
Если высказывание истинно, говорят, что его истинностное значение есть И («истина»), а если высказывание ложно, то его истинностное значение есть Л («ложь»). В английской литературе T (“true”) иF (“false”).
Высказывание 2x2 = 4 имеет истинностное значение И, а высказывание «Рим — столица Франции» — Л.
Однако, не каждое повествовательное предложение является высказыванием. Рассмотрим предложение: «Остаток от деления числа п на 7 равен 3». В этом предложении не содержится никакого утверждения. Нельзя ставить вопрос о его истинности и ложности. Однако, подставив в это предложение вместо п обозначение какого-либо конкретного натурального числа, мы получим высказывание. Буква n, входящая в это предложение, играет роль переменной. Вообще, переменная — это языковое выражение, служащее для обозначения произвольного объекта из некоторого фиксированного множества, называемого областью возможных значений этой переменной. Если переменная употребляется таким образом, что допускается подстановка вместо нее обозначений (имен) объектов из области ее возможных значений, то эта переменная называется свободной. Таковы, например, переменные x,y,z в выражениях х < у и z = i+l. Однако в математике встречается такое употребление переменных, при котором не предполагается и не допускается возможность подстановки вместо них имен конкретных объектов.
Например, в выражение 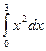 , где х — действительная переменная, т.е. переменная, областью возможных значений которой является множество действительных чисел, нельзя подставлять вместо х обозначения каких-либо конкретных действительных чисел.
, где х — действительная переменная, т.е. переменная, областью возможных значений которой является множество действительных чисел, нельзя подставлять вместо х обозначения каких-либо конкретных действительных чисел.
Вот другой пример: «Не существует такого рационального числа q, что q2 = 2». Хотя это предложение и содержит переменную q, подстановка в него обозначений каких-либо чисел вместо q не имеет смысла. В том случае, когда по смыслу выражения, содержащего переменную, подстановка вместо нее имен конкретных объектов недопустима, эта переменная называется связанной. В одном выражении одна и та же переменная может употребляться и как свободная, и как связанная.
Например, в выражении  оба вхождения переменной х в подынтегральное выражение являются связанными, а ее вхождение в качестве верхнего предела интегрирования — свободным. Вообще, следует говорить именно о свободных и связанных вхождениях данной переменной в данное выражение.
оба вхождения переменной х в подынтегральное выражение являются связанными, а ее вхождение в качестве верхнего предела интегрирования — свободным. Вообще, следует говорить именно о свободных и связанных вхождениях данной переменной в данное выражение.
Выражение, содержащее свободные вхождения переменных и превращающееся в имя некоторого объекта (или, соответственно, высказывание) всякий раз, когда вместо всех свободных вхождений каждой переменной подставляется имя какого-нибудь объекта из области ее возможных значений, называется именной формой (или, соответственно, высказывательной формой). Переменные, имеющие свободные вхождения в именную или высказывательную форму, называются ее параметрами. Именную или высказывательную форму будем называть k-местной, если она содержит ровно к различных параметров. В частности, можно говорить и о 0-местных именных и высказывательных формах, понимая под ними соответственно имена и высказывания.
Иногда для k-местной именной или высказывательной формы мы будем употреблять обозначение вида F(x1, x2,..., xk), явно указывая все ее параметры. Тогда, если a1, a2,..., ak — имена каких-либо объектов из областей возможных значений переменных x1, x2,..., xk соответственно, то через F(a1, a2,..., ak.) обозначается выражение, полученное из F(x1, x2,..., xk) подстановкой a1 вместо x1 и т. д.
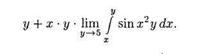
|
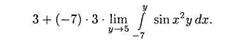
|
| Вообще, F(a, b) имеет вид |
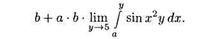
|
| Пример 2. Через A(i, к, m) обозначим высказывательную фор- |
| му |
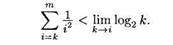
|
| Тогда, например, A (5,2,8) есть высказывание |
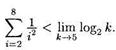
|
Пример 1. Через F(x,у) обозначим именную форму
Тогда F(—7,3) есть выражение (имя)
Логические операции
Из одних высказываний различными способами можно строить новые более сложные высказывания. Способ построения сложного высказывания из данных высказываний, при котором истинностное значение сложного высказывания полностью определяется истинностными значениями исходных высказываний, называется логической операцией.
Примером логической операции может служить отрицание, преобразующее любое данное высказывание А в высказывание «Неверно, что А», которое мы будем обозначать ¬А. Высказывание ¬А истинно тогда и только тогда, когда А ложно. Этот факт можно выразить посредством следующей истинностной таблицы:
| А ¬А И Л Л И |
Эта таблица показывает, какое истинностное значение имеет высказывание ¬А при данном истинностном значении высказывания А.
Вообще, для любой логической операции можно построить соответствующую ей истинностную таблицу. Некоторые из наиболее употребительных логических операций имеют специальные названия и обозначения. Кроме отрицания(┐, ¬, ¯), это еще двуместные операции: конъюнкция (&,∧), дизъюнкция (∨), импликация (É,→,=>), эквивалентность (≡, ↔, <=>). Им соответствуют следующие истинностные таблицы:
| А В | А & B | A ∨ B | A → В | А ≡ В |
| И И | И | И | И | И |
| И Л | Л | И | Л | Л |
| Л И | Л | И | И | Л |
| Л Л | Л | Л | И | И |
В математической логике принято не различать логические операции с одинаковыми истинностными таблицами независимо от того, какое словесное оформление имеют эти логические операции. Например, высказывание A ⊃ В может передаваться посредством выражений «Если А, то В», «А влечет В», «В случае А имеет место В», «Для А необходимо В», «А, только если В» и т. п. Вот языковые эквиваленты для других логических операций:
¬А — «Не А», «А не имеет места», «А неверно»;
A & В — «А и В», «Не только А, но и В», «Как А, так и В»;
А ∨ В — «А или В или оба», «А или В», «А, если не В»;
А ≡ В — «А, если и только если В», «Если А, то и В, и обратно», «А эквивалентно В», «А равносильно В». «А тогда и только тогда, когда В».
Наконец, приведем пример операции над высказываниями, которая не является логической операцией: по высказыванию А строим высказывание «Я знаю, что А». Очевидно, что истинность или ложность такого высказывания зависит не только от истинностного значения А, но и от осведомленности субъекта, произносящего это высказывание.
Рассмотренные нами логические операции ¬, ∧, ∨, ≡,⊃, называются пропозициональными операциями, а символы используемые для их обозначения, — пропозициональными связками. Эти операции можно, очевидно, применять и к высказывательным формам, получая из них более сложные высказывательные формы.
Упражнение. Найти истинностные значения следующих высказываний:
а) Если 11 делится на 3, то 11 делится на 6.
б) Если 15 делится на 3, то 15 делится на 6.
в) 11 делится на 3 тогда и только тогда, когда 15 делится на 6.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 349; Нарушение авторских прав?; Мы поможем в написании вашей работы!