Некоторые законы распределения случайных величин

Случайная величина, представленная совокупностью отдельных значений, может иметь тот или иной закон распределения.

Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

В теории и практике надежности чаще всего используются следую­щие законы распределения: нормальный (Гаусса), логарифмически нормальный, Вейбулла, экспоненциальный (показательный) и др.

Интегральная функция распределения имеет вид

. (3.8)

Дифференциальная функция распределения, или плотность распределения, есть производная от интегральной функции:

. (3.9)

Нормальный закон распределения (рис. 3.1) встречается достаточно часто. Плотность распределения его находят по выражению:

. (3.10)

Величина­­ Х (среднее ариф­метическое) показывает смещение кривой f(х) вдоль оси абсцисс без изменения ее формы, т. е. расстоя­ние от начала координат до абс­циссы с максимальной ординатой.

Величина (среднее квадра­тичное отклонение) показывает разброс отдельных значений случайной величины х относи­тельно сред­него арифметиче­ского Х. На участке кривой, ограниченной ординатами + и - (рис. 3.1), расположено 68,3% значений случайной величины; на участке, ограниченном ординатами +2, -2, -95,4%; на участке с ординатами +3 и -3 - 99,7%. На этом основано правило трех сигм:

вероятность того, что случайная величина х лежит в пределах 3, близка к единице или к 100%. Следовательно, значения случайной величины, лежащие за пределами 3, можно отбросить как промахи [8].

Если в качестве аргумента в формуле (3.10) принять безразмерную переменную

, (3.11)

Рис. 3.1. Нормальный закон то получим стандартный закон

распределения нормального распределения [6-8].

. (3.12)

Нормальный закон наблюдается в тех многочисленных случаях, когда на измеряемую случайную величину действуют разнообразные факторы, не связанные между собой и равнозначно действующие на случайную величину (например, размеры и износы деталей, наработки на отказ и до предельного состояния, причинами которых являются износы и т. д.).

Логарифмически нормальным называется распределение случайной величины y, если десятичный логарифм этой величины распределяется по нормальному закону. При этом в формуле (3.10) x = log y.

Закон распределения Вейбулла (рис. 3.2) описывается дифференциальной функцией:

, (3.13)

где m, a — параметры распределения.

Значение параметра m зависит от коэффициента вариации и определяется по таблицам [4, 6, 8, 10], расчетом или графоаналитическим путем. Величина его влияет на форму дифференциальной кривой.

При m = 1 распределение Вейбулла преобразуется в экспоненциаль­ное, при m = 2,5...3,5 и V = 0,3...0,4 — приближается к нормальному. Распределение Вейбулла широко применяется при расчете показателей надежности, в частности, при исследовании прочности и долговечности деталей. Этому закону хорошо подчиняются распределение предела уп­ругости ряда металлов, характеристики прочности и усталостной долго­вечности деталей (подшипники качения, напряженные оси и валы и др.).

Дифференциальная функция экспоненциального закона (рис. 3.3) имеет вид

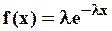, (3.14)

где — параметр распределения (постоянный коэффициент).

У экспоненциального распределения математическое ожидание и среднее квадратичное отклонение одинаковы:

. (3.15)

Поэтому коэффициент вариации равен единице.

Этот закон характерен для распределения случайных величин, изменение которых обусловлено влиянием какого-то доминирующего фактора. Он используется при рассмотрении внезапных отказов деталей в тех случаях, когда явления изнашивания и усталости выражены настолько слабо, что ими можно пренебречь (например, наработка до отказа многих невосстанавливаемых изделий).

Дата добавления: 2014-01-20