Точка принадлежит поверхности, если принадлежит какой-либо линии на этой поверхности

Линейчатые поверхности с двумя направляющими и плоскостью параллелизма (поверхности Каталана.)

а) Поверхность прямого цилиндроида Ф(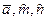)[A],

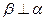где n - плоская кривая (n ) и (плоскость параллелизма)

б) Поверхность прямого коноида Ф(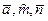)[A], где n

в) Поверхность гиперболического параболоида (косая плоскость)

Ф(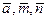)[A]

Пример: Поверхность прямого коноида

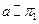
(a –параллельна π₁₎

Линейчатые поверхности с одной направляющей

(торсы.)

Торсы -развертываемые поверхности

а) Поверхность с ребром возврата. Образуются движением прямой, касательной во всех положениях к пространственной кривой.

б) Цилиндрическая поверхность. Образующие пересекаются в несобственной точке S,направляющая – кривая линия.

Цилиндр - круговой,

если в нормальном

сечении -окружность.

Эллиптический – если

в нормальном сечении-

эллипс.

Цилиндр – параболический,

гиперболический, эвольвентный

и т.д.

в) Коническая поверхность

Все образующие

пересекаются в

одной точке.

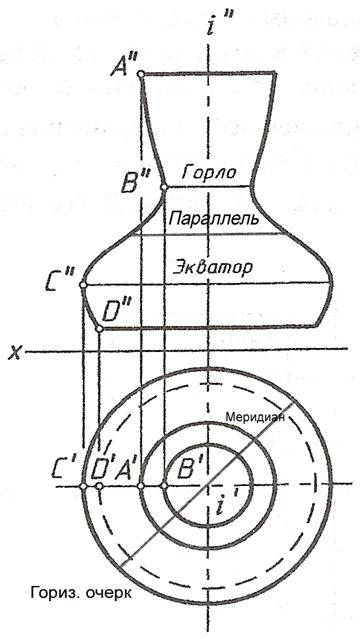
Поверхности вращения

Поверхность – получаемая вращением какой-либо образующей вокруг неподвижной оси.

Частные виды поверхностей вращения

1. Цилиндр вращения – образующая a параллельна оси i.

2. Конус вращения – образующая a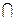i = S

3. Сфера – образующая окружности – центр Oi.

4. Тор – образующая – окружность (открытый тор) или дуга (закрытый тор или самопересекающийся), центр O i.

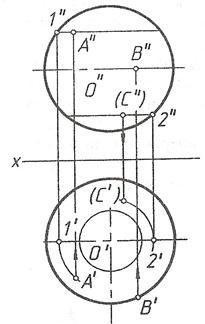
гиперболоид вращения (образующая – гипербола).

Винтовые линейчатые поверхности -

-образуются винтовым движением образующей a (т.е. вращением вокруг оси и одновременно поступательным движением.)

Поверхность – геликоид прямой, если 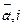==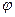90⁰ и косой – если =,

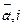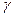где 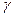0< <90⁰

Поверхности нелинейчатые

Нелинейчатые поверхности подразделяют на поверхности с образующей переменного вида (изменяющейся в процессе движения) и образующей постоянного вида.

Нелинейчатые поверхности с образующей переменного вида.

а) поверхность общего вида

б) каналовая поверхность – образована движением плоской замкнутой линии, определённым образом ориентированной в пространстве.(вентиляционные трубы).

в) циклическая – частный случай каналовой, когда образующая – окружность с монотонно изменяющимся радиусом.

Нелинейчатые поверхности с образующей постоянного вида

а) поверхность общего вида

образующая – произвольная кривая

детская горка

б) трубчатая поверхность

образующая – окружность постоянного радиуса, плоскость её перпендикулярна к направляющей.

Пример: трубка,шланг.

Дата добавления: 2014-01-20