Интегрирование рациональных дробей. – дробная рациональная функция

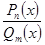– дробная рациональная функция. Правильная, если п < m, и неправильная в обратном случае.

Заметим, что из неправильной дроби модно выделить целую часть и представить неправильную дробь в виде суммы многочлена и правильной дроби.

Среди всех правильных дробей выделяют элементарные и простые дроби.

Элементарные дроби – это дроби вида: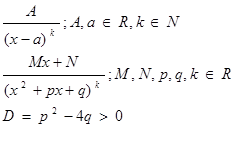

Интегрирование элементарных дробей:

Интегрирование элементарных дробей:

1.

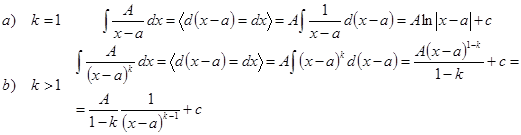
2.

***

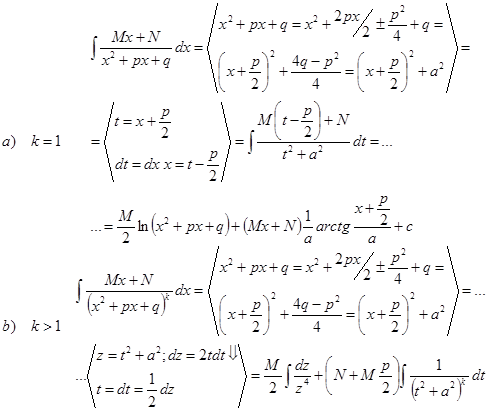
Вопрос №50: Интегрирование тригонометрических и иррациональных выражений:

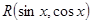– дробное рациональное выражение от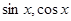

Интегрирование производится с помощью универсальной подстановки:

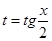
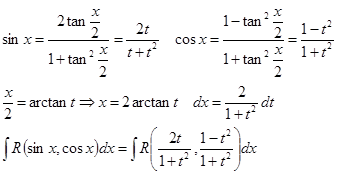
Однако эта замена иногда приводит к очень сложным выражениям, по этом модно предложить другую замену:

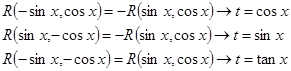
Так же можно применять тригонометрические преобразования:

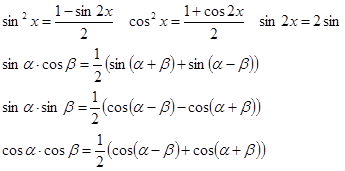
Интегрирование иррациональности:

Основная идея заключается в том, что бы рационализировать подынтегральное выражение.

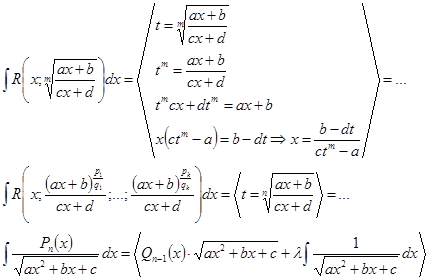
Многочлен п-1 -ой степени с неопределёнными коэффициентами.

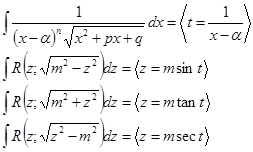
Вопрос № 51: Задачи, приводящие к определённому интегралу:

Физический смысл интеграла:

Пусть 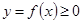представляет собой закон скорости движения материальной точки вдоль оси ординат. Ставится задача вычислить путь между двумя пунктами, который проходит точка.

Отрезок разбивается на малые промежутки, число которых стремится к бесконечности. В этом случае путь считается, как сумма значений функции на этих промежутках. При увеличении числа промежутков на отрезке, получаемая сумма будет стремиться к истинному значению пути.

В этом случае путь нужно считать, как предел суммы значений функции на атом отрезке.

Вопрос № 52: Интегральные суммы:

1. Интегральные суммы.

2. Определённый интеграл.

3. Геометрический смысл.

4. Свойства, связанные с равенствами.

5. Понятие подынтегральной функции.

Геометрический смысл интеграла:

Геометрический смысл интеграла представляет собой площадь фигуры – кривой, состоящей из бесконечного количества прямоугольников.

Эта площадь приблизительно равна площади криволинейной трапеции.

Построение определённого интеграла:

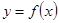определена на отрезке. Разобьём его на малые части и возьмём н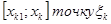а тогда
Число 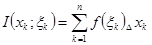– называется определённым интегралом для функции 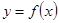на отрезке.

Число 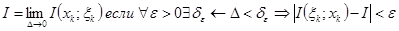– называется определённым интегралом для функции на отрезке, и обозначается: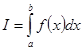

Классификация интегрируемых функций:

1. Если функция непрерывна на отрезке, то она интегрируема на нём.

2. Если функция монотонная и ограничена на отрезке, значит она интегрируема на нём.

Свойства определенного интеграла:

1.

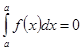
2.

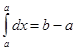
3.

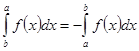
4. Если две различные функции интегрируемы на отрезке, значит их сумма, разность, произведение так же интегрируема на отрезке.

5. Если функция имеет интеграл на отрезке, значит произведение функции на константу так же имеет интеграл.

6. Если функция интегрируема на отрезке, то она интегрируема на всех отрезках, входящих в первый.

Оценки интегралов:

1.Если функция интегрируема на отрезке, неотрицательна, для х из отрезка, тогда её интеграл на отрезке так же неотрицателен. Действительно все интегральные суммы больше, либо равны нулю, а по свойству их общий придел больше, либо равен нулю.
Следствие:

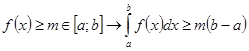
2.Если функция непрерывна и неотрицательна на отрезке, то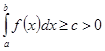

3.Если две различные функции интегрируемы на отрезке, и первая больше второй, то интеграл от первой будет больше интеграла от второй на отрезке.
Следствие:
Если функция интегрируема на отрезке, то модуль функции так же интегрируем на отрезке, и имеет место оценка, что модуль интеграла функции меньше, либо равен интегралу модуля функции.

Теорема о среднем:

Функция интегрируема на отрезке.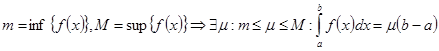

Доказательство:

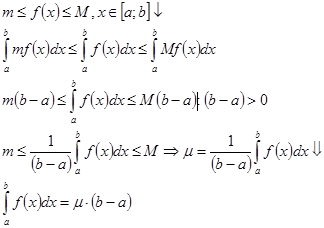
Следствие:

Если функция непрерывна на отрезке, то существует ξ из отрезка, для которой 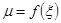, тогда 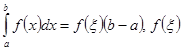– среднее значение функции на отрезке.

Вопрос № 54: Определённый интеграл с переменным верхним пределом:

1.Определённый интеграл с переменным верхним пределом.

2.Свойства.

3.Доказательство формулы Ньютона-Лейбница.

Пусть функция интегрируема на отрезке, фиксируем точку С из отрезка. Для всех х функция интегрируема на отрезке 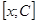, тогда на отрезке 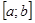определена функция 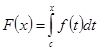– это интеграл с переменным верхним пределом.

Если функция непрерывна на отрезке, то для неё существует первообразная на этом отрезке, одной из первообразных является функция 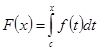, следовательно:

1.

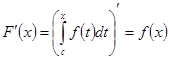
2. Функция 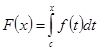непрерывна на отрезке .

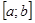Заметим, что в выражении точка С – любая точка из отрезка.

Основная формула интегрального исчисления:

Было доказано, что две любые первообразные от функции отличаются на константу, тогда любую первообразную для функции можно представить в виде:
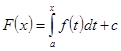, вычислив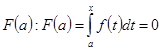

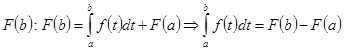
Вопрос № 55: Интегрирование по частям и замени переменной в определённом интеграле:

Замена переменной в определённом интеграле:

Замена переменной в определённом интеграле производится так же, как и в неопределённом, только необходимо пересчитать пределы интегрирования, подставив их в подстановочную формулу.

Интегрирование по частям в определённом интеграле:

Для 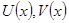на отрезке существуют непрерывные производные, тогда

Доказательство:

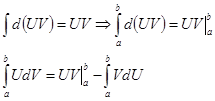
Вопрос № 56: Приложение определённого интеграла к вычислению площадей плоских фигур и длин дуг:

Площадь плоской фигуры:

Функция неотрицательна на отрезке, тогда из геометрического смысла определённого интеграла следует, что площадь, вычисляется по формуле .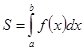

Пусть функция задана параметрически, неотрицательна на отрезке, и существуют и непрерывны первые производные 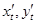, то площадь такой фигуры –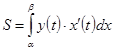

Площадь криволинейного сектора:

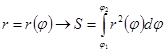
Длинна дуги:

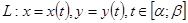, производные непрерывны на отрезке, тогда кривая спрямляема, и её длинна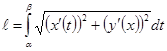

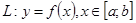, производная функции непрерывна на отрезке, тогда кривая спрямляема, и её длинна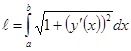

Пусть прямая задана в полярной системе координат, производная функции непрерывна на заданном отрезке, тогда кривая спрямляема, и её длинна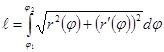

Длинна дуги пространственной прямой:
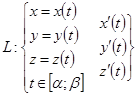– непрерывны на отрезке, тогда кривая спрямляема, и её длинна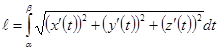

Вопрос № 57: Вычисление площадей поверхностей тел вращения:

1. Вычисление площадей поверхностей тел вращения.

2. Вычисление объёмов тел вращения.

3. Вычисление объёмов тел по известным поперечным сечениям.

Объём тел вращения:

При вращении криволинейной трапеции вокруг оси Х и вокруг оси У получаются различные объёмы.

Пусть функция неотрицательна на отрезке, и непрерывна на нём, тогда объёмы

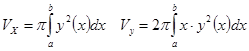
Более общий случай:

Пусть заданы две функции, причём одна больше, либо равна другой, и обе неотрицательны на отрезке, тогда

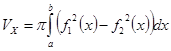
Пусть заданы две функции, причём одна больше, либо равна другой, отрезок лежит, целиком, правее от начала отсчёта, тогда

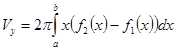
В параметрическом виде:

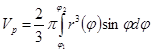
Объём тела с известной площадью поперечного сечения:

Пусть некоторое ограниченное тело лежит над отрезком оси ОХ. При произвольном х из отрезка рассечём тело перпендикулярно оси.

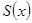– площадь сечения, если она непрерывна на отрезке, то объём можно найти по формуле:

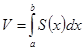
Площадь поверхности вращения:

При вращении криволинейной трапеции вокруг оси, она описывает поверхность, площадь которой:

1.

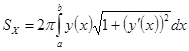
2.

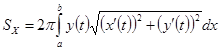
3.

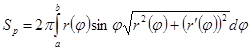
Вопрос № 58: Несобственный интеграл с бесконечным пределом интегрирования:

1. Несобственный интеграл с бесконечным пределом интегрирования.

а)Определение.

б) Сходимость.

2.Понятие о неопределённом интеграле от функции, неограниченной на отрезке интегрирования.

3.Свойства.

[1] Замкнутое ограниченное множество в называется «компактом»

[2] равномерно непрерывна на, если для всех такая, что для всех точек М_1,2 из

Дата добавления: 2014-01-11