Лекция 1. Определение 1.Линейное программирование – наука о методах исследования и отыскания экстремальных значений линейной функции

ВВЕДЕНИЕ

Определение 1. Линейное программирование – наука о методах исследования и отыскания экстремальных значений линейной функции, на неизвестные которой наложены линейные ограничения

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

Определение 2. Математическое выражение целевой функции и её ограничений называется математической моделью экономической задачи.

Определение 3. Допустимым решением задачи линейного программирования называется вектор , удовлетворяющий системе ограничений.

Определение 4. Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением задачи линейного программирования и обозначается .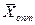

Определение 5. Если все ограничения системы заданы уравнениями и переменные 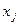неотрицательные, то такая модель задачи называется канонической.

Если хотя бы одно ограничение является неравенством, то модель задачи ЛП является неканонической.

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В п -МЕРНОМ ПРОСТРАНСТВЕ

Определение 1. Множество точек п -мерного пространства, координаты которых удовлетворяют уравнению , где хотя бы одно из чисел 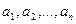отлично от нуля, называется гиперплоскостью п-мерного пространства.

Определение 2. Множество точек п -мерного пространства, координаты которых одновременно удовлетворяют каждому уравнению системы

,

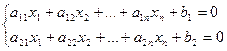называется пересечением гиперплоскостей.

Определение 3. Множество точек п -мерного пространства, координаты которых удовлетворяют неравенству 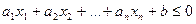, называется полупространством п -мерного пространства, расположенным по одну сторону от гиперплоскости .

Определение 4. Множество точек п -мерного пространства, содержащее вместе с любыми двумя точками А и В и все точки отрезка АВ, называется выпуклым телом (областью, фигурой).

Определение 5. Точка А называется внутренней точкой выпуклой области, если в сколь угодно малой окрестности этой точки содержатся только точки этой области.

Определение 6. Точка В называется граничной точкой выпуклой области, если в сколь угодно малой окрестности этой точки содержатся как точки данной области, так и не принадлежащие ей.

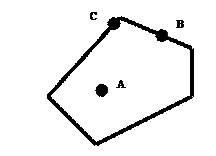Определение 7. Точка С называется угловой точкой выпуклой области, если она является граничной и не лежит внутри отрезка, соединяющего две другие точки этой области.

Определение 8. Если область включает все свои граничные точки, то она называется замкнутой.

Определение 9. Ограниченной называется область, если существует такое число М > 0, что радиус-вектор 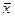, соединяющий начало координат с любой точкой области, по абсолютной величине меньше М, т. е. .

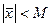Определение 10. Если найдутся точки области, сколь угодно удалённые от начала координат, то область называется неограниченной.

Определение 11. Выпуклая замкнутая ограниченная область, имеющая конечное число угловых точек, называется выпуклым п-мерным многогранником.

Определение 12. Выпуклая замкнутая неограниченная область, имеющая конечное число угловых точек, называется выпуклой п-мерной многогранной областью.

Определение 13. Линейная комбинация S векторов , в которой коэффициенты удовлетворяют условиям 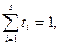, называется выпуклой линейной комбинацией.

Определение 14. Пересечением выпуклых областей называется множество точек, являющееся общей частью этих областей.

Теорема 1. Пересечение выпуклых областей есть выпуклая область.

Теорема 2. Множество точек выпуклого п-мерного многогранника совпадает с множеством любых выпуклых линейных комбинаций его угловых точек.

Дана система .

Прямая , а также остальные прямые, соответствующие неравенствам данной системы, называются граничными прямыми.

Определение 15. Решением каждого неравенства системы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от неё.

Определение 16. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы (ОР).

Определение 17. Область решения системы, удовлетворяющая условиям неотрицательности, называется областью неотрицательных, или допустимых, решений (ОДР).

Дата добавления: 2014-01-11