Лекция 2. Пример 1.Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР

НАХОЖДЕНИЕ ОБЛАСТИ РЕШЕНИЕ И ОБЛАСТИ ДОПУСТИМЫХ РЕШЕНИЙ

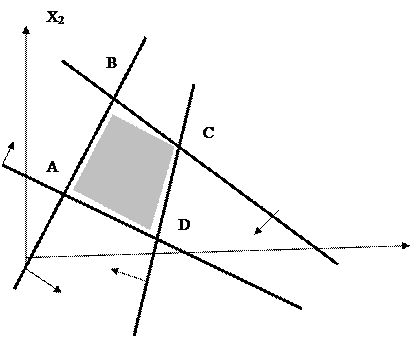
Пример 1. Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР

Ответ: А(3/7, 6/7), В(5/3, 10/3), С(11/4, 9/4), D(21/10, 3/10), ОР и ОДР совпадают.

		Х1

Пример 2. Найти ОР и ОДР системы неравенств

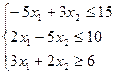
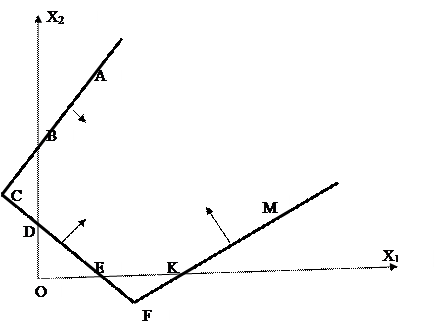Ответ: ACFM – ОР, ABDEKM – ОДР.

Пример 3. Найти ОР и ОДР системы неравенств

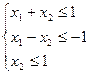
Ответ:ABC – ОР, точка B – ОДР.

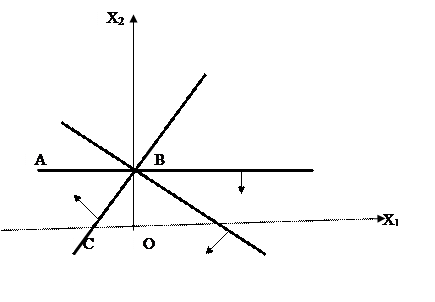
Пример 4. Найти ОР и ОДР системы неравенств

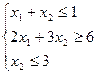
Ответ: ОР и ОДР несовместны.

ГРАФИЧЕСКИЙ МЕТОД

1. Находим область допустимых решений системы ограничений задачи.

2. Строим вектор 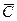, координатами которого являются коэффициенты целевой функции.

3. Проводим линию уровня 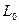, которая перпендикулярна.

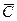4. Линию уровня перемещаем по направлению вектора 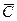для задач на максимум и в направлении, противоположном 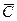, для задач на минимум.

Перемещение линии уровня производится до тех пор, пока у неё не окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума.

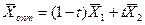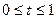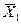Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум, и её решение находится по формуле , где , и 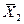- оптимальные решения в угловых точках ОДР.

Задача ЛП может быть неразрешима, когда определяющие её ограничения окажутся противоречивыми.

5. Находим координаты точки экстремума и значение целевой функции в ней.

Дата добавления: 2014-01-11