
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод произведений для вычисления выборочных средней и дисперсии
|
|
|
|
Метод произведений дает удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Через найденные условные моменты впоследствии не сложно вычислить начальные и центральные моменты. Методом произведений легко находить выборочные среднюю и дисперсию. Для удобства вычислений пользуются таблицей, которая составляется следующим образом:
- в первый столбец записывают выборочные варианты
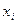 , расположенные в возрастающем порядке,
, расположенные в возрастающем порядке, - во второй столбец записывают частоты вариант
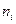 , их сумму (по столбцу)
, их сумму (по столбцу)  помещают в последнюю клетку второго столбца,
помещают в последнюю клетку второго столбца, - в третий столбец записывают условные варианты
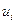 , причем в качестве ложного нуля С выбирают варианту с наибольшей частотой (шаг
, причем в качестве ложного нуля С выбирают варианту с наибольшей частотой (шаг 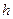 полагают равным разности между соседними вариантами),
полагают равным разности между соседними вариантами), - в четвертый столбец записывают произведение частот на условные варианты
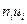 , их сумму (по столбцу)
, их сумму (по столбцу)  помещают в последнюю клетку четвертого столбца,
помещают в последнюю клетку четвертого столбца, - в пятый столбец записывают произведения частоты на квадраты условных вариант
 , их сумму (по столбцу)
, их сумму (по столбцу) 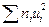 помещают в последнюю клетку пятого столбца,
помещают в последнюю клетку пятого столбца, - в шестой столбец записывают произведение частоты на квадраты условных вариант, увеличенных (каждая) на единицу
 , их сумму (по столбцу)
, их сумму (по столбцу)  помещают в последнюю клетку шестого столбца, при этом шестой столбец используется лишь для контроля правильности вычислений:
помещают в последнюю клетку шестого столбца, при этом шестой столбец используется лишь для контроля правильности вычислений:
 .
.
После заполнения таблицы вычисляют условные моменты:
 ,
, 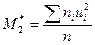
и по ним определяют выборочную среднюю и выборочную дисперсию:
 ,
,
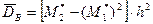 .
.
Пример. Найти методом произведений выборочные среднюю и дисперсию следующего статистического распределения:
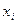
| 10,2 | 10,4 | 10,6 | 10,8 | 11,0 | 11,2 | 11,4 | 11,6 | 11,8 | 12,0 |
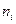
|
Составим расчетную таблицу:
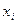
| 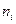
| 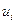
| 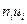
| 
| 
|
| 10,2 | -4 | -8 | |||
| 10,4 | -3 | -9 | |||
| 10,6 | -2 | -16 | |||
| 10,8 | -1 | -13 | |||
| 11,0 | |||||
| 11,2 | |||||
| 11,4 | |||||
| 11,6 | |||||
| 11,8 | |||||
| 12,0 | |||||
 =100 =100
|  =57 =57
| 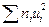 =383 =383
|  =597 =597
|
Вычисления проведены корректно, т.к. выполнено соотношение:
 .
.
Найдем условные моменты первого и второго порядков:

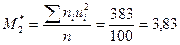 .
.
Определим выборочные среднюю и дисперсию:

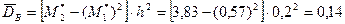 .
.
Сведение первоначальных вариант к равноотстоящим
На практике, как правило, эмпирические данные не являются равноотстоящими числами. Для удобства расчетов их необходимо свести к равноотстоящим. Для этого интервал, в котором заключены исходные варианты, делится на несколько равных «частичных» интервалов (на практике в каждый частичный интервал должно попасть не менее 8-10 первоначальных вариант). Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант. В качестве частоты каждой новой варианты (середины частичного интервала) принимают общее число первоначальных вариант, которые попали в соответствующий частичный интервал.
Пример. Выборочная совокупность объема n =100 задана следующей таблицей:
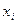
| 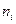
| 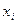
| 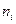
| 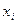
| 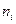
|
| 1,00 | 1,19 | 1,37 | |||
| 1,03 | 1,20 | 1,38 | |||
| 1,05 | 1,23 | 1,39 | |||
| 1,06 | 1,25 | 1,40 | |||
| 1,08 | 1,26 | 1,44 | |||
| 1,10 | 1,29 | 1,45 | |||
| 1,12 | 1,30 | 1,46 | |||
| 1,15 | 1,32 | 1,49 | |||
| 1,16 | 1,33 | 1,50 |
Необходимо составить таблицу равноотстоящих вариант.
Интервал изменения вариант разбивается на 5 (к примеру) частичных интервалов:
| 1,00-1,10 | 1,10-1,20 | 1,20-1,30 | 1,30-1,40 | 1,40-1,50 |
Примем середины частичных интервалов в качестве новых вариант 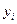 , которые будут равноотстоящими:
, которые будут равноотстоящими:

| 
| 
| 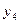
| 
|
| 1,05 | 1,15 | 1,25 | 1,35 | 1,45 |
Найдем частоты новых вариант 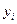 :
:
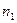
| 
| 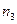
| 
| 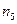
|
Т.е. 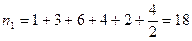 ,
,  …
…
Таким образом, имеем следующее распределение равноотстоящих вариант:
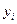
| 1,05 | 1,15 | 1,25 | 1,35 | 1,45 |
|
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2275; Нарушение авторских прав?; Мы поможем в написании вашей работы!