Сетевые модели

Современное сетевое планирование начинается с разбиения программы работ на операции. Определяются оценки продолжительности операций и строится сетевая модель. Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала её реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями графика. Календарный график выявляет критические операции, которым надо уделять особое внимание, чтобы закончить все работы в положенный срок. По некритическим операциям календарный план позволяет определить резервы времени, которые можно выгодно использовать.

Основные операции сетевой модели

Сетевая модель – графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа. Граф – схема, состоящая из заданных точек (вершин), соединённых системой линий. Отрезки, соединяющие вершины, называются рёбрами графа. Ориентированным называется такой граф, на котором стрелкой указаны направления всех его рёбер, что позволяет определить, какая из двух его граничных вершин является начальной, а какая – конечной.

Работа – это активный процесс, требующий затрат ресурсов, либо пассивный, приводящий к достижению намеченного результата.

Фиктивная работа – это связь между результатами работ, не требующая затрат времени и ресурсов.

Событие – это результат выполнения одной или нескольких предшествующих работ.

Путь – это любая непрерывная последовательность работ и событий. Контур – путь, у которого начальная вершина совпадает с конечной. Сетевой график – это ориентированный граф без контуров.

Критический путь – это путь, не имеющий резервов и включающий самые напряжённые работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.

При построении сетевых моделей необходимо соблюдать следующие правила.

1. Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.

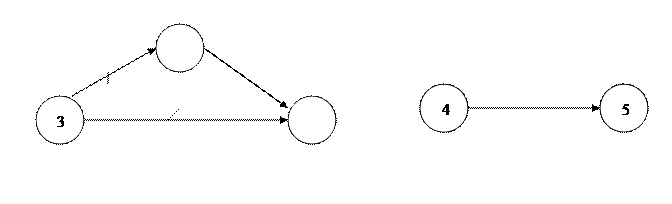
2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис 1).

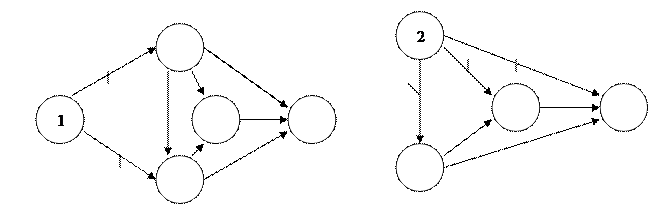
3. В сети не должно быть тупиков, т. е. промежуточных событий, из которых не выходит ни одна работа (рис 2).

4. В сети не должно быть промежуточных события, которым не предшествует хотя бы одна работа (рис. 3).

5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 4). Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому даётся номер 1. Из исходного события 1 вычёркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию даётся номер 2. Затем вычёркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события.

Рис.5.

Пример нумерации сетевого графика (рис. 5).

Рассмотрим программу создания нового бытового прибора, пользующегося спросом у населения. Необходимые данные приведены в таблице.

Операции	Наименование работы	Непосредственно предшествующие операции	Продолжительность, неделя
А, Б     В, Г     Д Е Ж   З, К   И	Разработка технической документации (ТД) на прибор и его электронную часть Разработка технологической документации на прибор и его электронную часть Передача ТД на прибор Изготовление приборов Изготовление электронной части прибора Разработка ТД на эксплуатацию прибора и электронную часть Сборка и испытания прибора	-     А, Б     А В, Д Д, Г   Г, В   Е, Ж	А – 3, Б – 2     В – 2, Г – 2       З – 5, К – 2

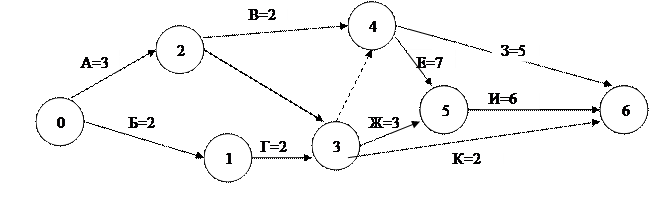
На основании данных таблицы построен сетевой график создания прибора с учётом вышеизложенных рекомендаций.

Расчёт временных параметров сетевого графика

Основным временным параметром сетевого графика является продолжительность критического пути.

Расчёт критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного события и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события определено одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.

Прямой проход:

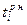- ранний срок начала всех операций, выходящих из события i.

Если i = 0, то 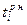= 0;

- ранний срок начала всех операций, выходящих из j. Тогда

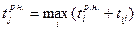для всех (i, j),

где t_ij – продолжительность операции (i, j);

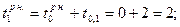
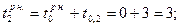
Обратный проход:

- поздний срок окончания всех операций, входящих в событие i.

Если i = п, где п – завершающее событие сети, то является отправной точкой обратного прохода;

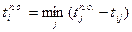для всех операций (i, j);

;

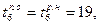
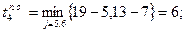
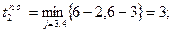
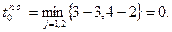
Используя результаты вычислений при прямом и обратном проходах, можно определить операции критического пути. Операция (i, j) принадлежит критическому пути, если она удовлетворяет условиям:

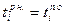
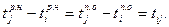
Для рассматриваемого примера критический путь включает операции (0, 2), (2, 3), (3, 4), (4, 5), (5, 6).

Операции связаны ещё двумя сроками:

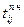- поздний срок начала работы. Он является наиболее поздним из допустимых моментов начала данной работы, при котором ещё возможно выполнение всех последующих работ в установленный срок:

- ранний срок окончания работы. Он является наиболее ранним из возможных моментов окончания работы при заданной продолжительности работ:

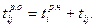
Различают два вида резервов времени: полный резерв (r_п) и свободный резерв (r_св).

Полный резерв времени показывает, на сколько может быть увеличена сумма продолжительности всех работ относительно критического пути. Он представляет собой разность между максимальным отрезком времени, в течение которого может быть выполнена операция, и её продолжительностью (t_ij) и определяется как

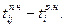
Свободный резерв времени – максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы при условии, что все события наступают в ранние сроки:

Результаты расчёта критического пути и резервов времени некритических операций представлены в таблице. Критические операции должны иметь нулевой полный резерв времени, при этом свободный резерв также должен быть равен нулю.

Работа (i,j)	Продол- житель- ность tij	Раннее	Позднее	Полный резерв rn	Свобод- ный резерв rсв	Ресурс Рабочей силы
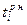
начало	оконча- ние	начало	оконча- ние
(0, 1) (0, 2) (1, 3) (2, 3) (2, 4) (3, 4) (3, 5) (3, 6) (4, 5) (4, 6) (5, 6)						0^к 0^к 0^к 0^к 0^к

Построение сетевого графика и распределение ресурсов

Конечным результатом выполняемых на сетевой модели расчётов является сетевой график. При построении сетевого графика необходимо учитывать наличие ресурсов, так как одновременное выполнение некоторых операций из-за ограничений, связанных с рабочей силой, оборудованием и другими видами ресурсов, иногда оказывается невозможным. Именно в этом отношении представляют ценность полные резервы времени некритических операций.

Сдвигая некритическую операцию в том или ином направлении, но в пределах её полного резерва времени, можно добиться снижения максимальной потребности в ресурсах. Однако даже при отсутствии ограничений на ресурсы полные резерв времени обычно используются для выравнивания потребностей в ресурсах на протяжении всего срока реализации программы работ. Это означает, что работы удастся выполнить более или менее постоянным составом рабочей силы.

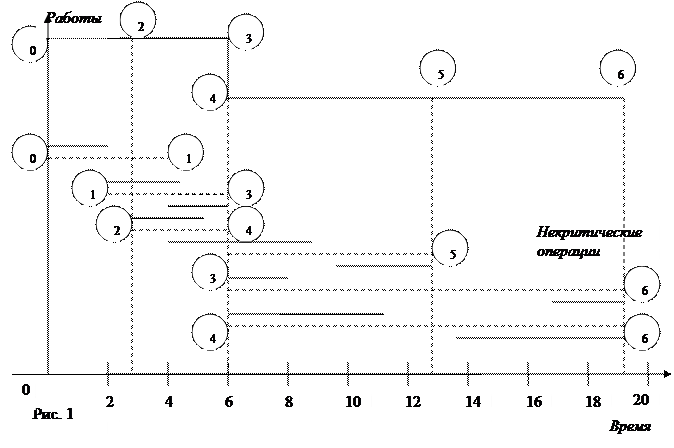
На рисунке 1 показан график рассмотренного примера. Роль полных и свободных резервов при выборе сроков объясняется двумя правилами:

1) если полный резерв равен свободному, то календарные сроки некритической операции можно выбрать в любой точке между её ранним началом и поздним окончанием;

2) если свободный резерв меньше полного, то срок начала некритической операции можно сдвинуть по отношению к раннему сроку её начала не более чем на величину свободного резерва.

В данном примере правило 2 применимо к операции (0, 1), а сроки всех остальных операций выбираются по правилу 1.

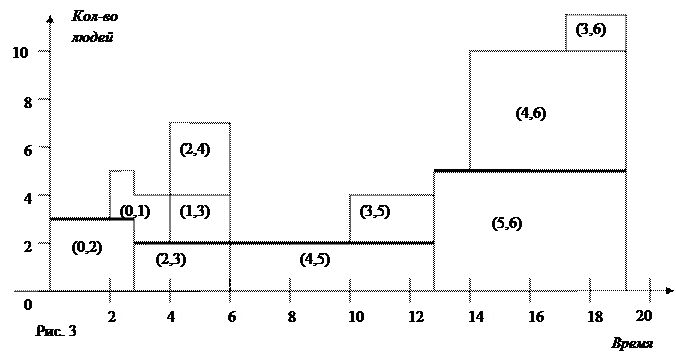
На рисунке 2 показана потребность в рабочей силе при условии выбора в качестве календарных сроков некритических операций начала их ранних сроков, на рисунке 3 – потребность в рабочей силе при выборе наиболее поздних сроков.

Жирной линией представлена потребность критических операций, которая должна быть удовлетворена, если нужно выполнить все работы в минимально возможный срок.

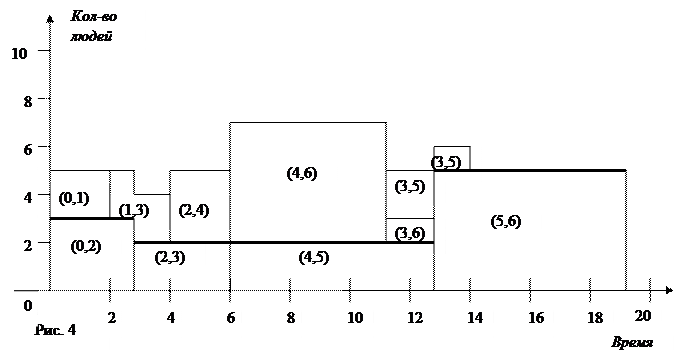
Оптимальное решение задачи равномерного использования ресурсов представлено на рисунке 4, уточнённый график выполнения работ на рисунке 5.

Учёт стоимостных факторов при реализации сетевого графика

Стоимостные факторы при реализации сетевого графика учитываются путём определения зависимости «затраты - продолжительность» для каждой операции. При этом рассматриваются прямые затраты, а косвенные типа административных или управленческих расходов не принимаются во внимание.

На рис. 6 показана линейная зависимость стоимости операции от её продолжительности. Точка (D_B, C_B), где D_B – продолжительность операции, а C_B – её стоимость, соответствует нормальному режиму выполнения операции. Продолжительность операции можно уменьшить (сжать), увеличив интенсивность использования ресурсов, а следовательно, увеличив стоимость операции. Однако существует предел, называемый минимальной продолжительностью операции. За точкой, соответствующей этому пределу (точка максимального интенсивного режима), дальнейшее увеличение интенсивности использования ресурсов ведёт лишь к увеличению затрат без сокращения продолжительности операции. Этот предел обозначен на рис. 6 точкой А с координатами (D_А, C_А).

Для удобства зависимость «затраты - продолжительность» принимается линейной, так как её можно определить для любой операции по двум точкам.

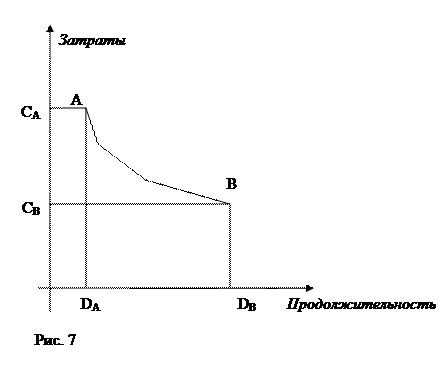Если зависимость не линейная, то её использовать гораздо сложнее, и поэтому её можно аппроксимировать (приблизить) кусочно-линейной зависимостью (рис. 7), когда операция разбивается на части, каждая из которых соответствует одному линейному отрезку. Наклоны этих отрезков при переходе от точки нормального режима к точке максимального режима возрастают. Если это условие не выполняется, то аппроксимация не имеет смысла.

Определив зависимость «затраты - продолжительность» для всех операций сети принимают нормальную продолжительность. Далее рассчитывается сумма затрат на все операции сети при этой продолжительности работ. На следующем этапе рассматривается возможность сокращения продолжительности работ. Этого можно достичь за счёт уменьшения продолжительности какой-либо критической операции. Анализу следует подвергать только критические операции.

Чтобы добиться сокращения продолжительности выполнения работ при минимально возможных затратах, необходимо в максимально допустимой степени сжать ту критическую операцию, у которой наклон кривой «затраты - продолжительность» наименьший. В результате сжатия критической операции получается новый календарный график, возможно, с новым критическим путём. Стоимость работ при новом календарном графике будет выше стоимость работ по предшествующему графику. На следующем этапе тот новый график вновь подвергается сжатию за счёт следующей критической операции с минимальным наклоном кривой «затраты - продолжительность» при условии, что продолжительность этой операции не достигла минимального значения. Данная процедура повторяется, пока все критические операции не будут находиться в режиме максимальной интенсивности. Полученный оптимальный календарный график соответствует минимуму прямых затрат.

Обоснование привлекательности проекта по выпуску продукции

Для финансирования проектов по строительству и наладке изготовления конкурентоспособной продукции в большинстве случаев фирмам требуются инвестиции. Включение в проект материалов с оптимизацией сетевых моделей в части обоснования сроков возврата инвестиций делает проект более привлекательным и способствует принятию инвестором положительного решения.

Пример. Предприятие решило для улучшения финансового состояния наладить выпуск конкурентоспособной продукции (мороженого). Для переоборудования цеха под выпуск этой продукции необходимо выполнить:

1) подготовку технического задания на переоборудование участка (30 дн.);

2) заказ и поставку нового оборудования (60 дн.);

3) заказ и поставку нового электрооборудования (50 дн.);

4) демонтаж старого и установку нового оборудования (90 дн.);

5) демонтаж старого и установку нового электрооборудования (80 дн.);

6) переобучение персонала (30 дн.);

7) испытания и сдачу в эксплуатацию оборудования для производства мороженого (20 дн.).

Ожидается, что производительность после ввода новой линии составит 20 т мороженого в смену. Прибыль от реализации 1 т продукции составит 0,5 тыс. р. В смену. Деньги на покупку и переоборудование участка в размере 2 000 тыс. р.взяты в банке под 20% годовых (из расчёта 1 500 тыс. р. на закупку оборудования и 500 тыс. р. на работы по демонтажу старого оборудования и установке нового оборудования). Затраты на проведение работ в нормальном и максимальном режимах указаны в табл.

Определить, через какое время может быть возвращён кредит в банк.

Работа	Нормальный режим	Максимальный режим
Продолжи- тельность, дн.	Затраты, тыс. р.	Продолжи- тельность, дн.	Затраты, тыс. р.
Итого

РЕШЕНИЕ. 1. Составим график проведения работ по пуску новой линии:

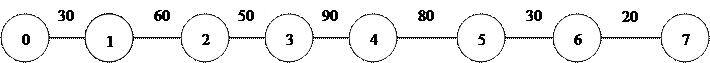
На проведение переоборудования необходимо 30 + 60 + 50 + 90 + 80 + 30 + 20 = 360 дн.

2. График можно улучшить, выполняя некоторые работы параллельно.

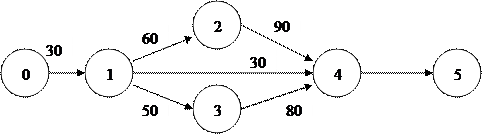На графике обозначены работы:

0, 1 – подготовка технического задания;

1, 2 – заказ и поставка нового оборудования;

1, 3 - заказ и поставка нового электрооборудования;

2, 4 – установка нового оборудования;

3, 4 - установка нового электрооборудования;

1, 4 – переобучение персона;

4, 5 – сдача в эксплуатацию новой линии.

По графику путь (0, 1), (1, 2), 2, 4), (4, 5) имеет продолжительность 200 дн.; (0, 1), (1, 3), (3, 4), (4, 5) – 180 дн.; (0, 1), (1, 4), (4, 5) – 80 дн.

Критическим путём графика является путь, на котором расположены работы (0, 1), (1, 2), 2, 4), (4, 5) продолжительностью 200 дн.

График улучшился на 360 – 200 = 160 дн.

Определим, через какое время после начала выпуска мороженого может быть возвращён кредит в банк.

Через 200 дн. После начала работ предприятие истратит 1 500 тыс. р. На приобретение оборудования (по условию) и 265 тыс. р. На его установку и сдачу в эксплуатацию (из табл., столбец «Затраты» при нормальном режиме). В наличии у предприятия остаётся

2000 – 1500 – 265 = 235 тыс. р.

Построим графики изменения кредита в зависимости от времени получения прибыли предприятием – от выпуска мороженого.

Для построения графика изменения кредита в зависимости от времени составим уравнение. Через 360 дн. После выдачи банком кредита под 20% годовых долг предприятия составит 2400 тыс. р. Поэтому известны две точки прямой А (0, 2000), В (360, 2400). Составим уравнение прямой, проходящей через две точки:

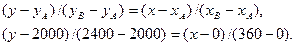
Решая уравнение, получим

Найдём уравнение прибыли предприятия. Известно, что через 200 дн. После начала работ у предприятия осталось от кредита 235 тыс. р. Через 100 дн. После начала выпуска продукции предприятие получит прибыль

тыс. р.

и у него будет в наличии

1000 + 235 = 1235 тыс. р.

Решение задач по теме «Сетевые модели» (работа в группах по 3 – 4 человека)

1. Составить сетевой график выполнения работ и рассчитать временные параметры по данным, представленным в таблице.

Содержание работы	Обозна- чения	Предыду- щая работа	Продолжи- тельность, дн.
Составление сметы Заказ и доставка оборудования Распределение кадров Установка оборудования Подготовка кадров Оформление торгового зала Доставка товаров Заказ и получение ценников Заказ и получение формы Выкладка товаров Заполнение ценников Генеральная репетиция	а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12	а1 а1 а2 а3 а4 а5 а5 а5 а6, а7 а8 а9, а10, а11

2. Постройте график работ, определите критический путь и стоимость работ при нормальном режиме, критический путь и минимальную стоимость работ при максимальном режиме. Исходные данные указаны в таблице.

Операция	Нормальный режим работ	Максимальный режим работ
Продолжи- тельность, дн.	Стоимость, ден. ед.	Продолжи- тельность, дн.	Стоимость, ден. ед.
1,2 1,3 1,4 2,4 2,6 3,4 3,5 4,6 5,6

3. Постройте график работ, определите критический путь и стоимость работ при нормальном режиме, критический путь и минимальную стоимость работ при максимальном режиме. Необходимые исходные данные указаны в таблице.

Операция	Нормальный режим работ	Максимальный режим работ
Продолжи- тельность, дн.	Стоимость, ден. ед.	Продолжи- тельность, дн.	Стоимость, ден. ед.
1,2 1,3 1,4 2,5 2,6 3,6 4,7 5,7 6,7

4. Для улучшения финансового состояния фирме необходимо увеличить спрос на выпускаемый цемент марки М400 и расширить потребительский рынок. Фирма считает целесообразным размещать цемент в специализированной таре. Для переоснащения цеха необходимо установить оборудование по производству специализированной тары. Предполагается выполнить следующее:

1) подготовку и выпуск технического задания на переоборудование цеха (20 дн.);

2) разработку мероприятий по технике безопасности (25 дн.);

3) подбор кадров (10 дн.);

4) заказ и поставку необходимого оборудования (30 дн.);

5) заказ и поставку электрооборудования (40 дн.);

6) установку оборудования (50 дн.);

7) установку электрооборудования (45 дн.);

8) обучение персонала (15 дн.);

9) испытание и сдачу в эксплуатацию линии (25 дн.).

Ожидается, что производительность вводимой линии по производству тары составит 1000 мешков в день при односменном режиме работы. Стоимость 1 мешка – 25 р., выручка от реализации тары в смену составит 25 тыс. р. Деньги на покупку оборудования и переоснащение цеха в размере 5500 тыс. р. взяты в банке под 30% годовых из расчёта 5000 тыс. р. На оборудование и 500 тыс. р. на его установку.

Затраты на проведение работ и их продолжительность в нормальном и максимальном режимах указаны в таблице.

Работа	Нормальный режим работ	Максимальный режим работ
Продолжи- тельность, дн.	Затраты, тыс. р.	Продолжи- тельность, дн.	Затраты, тыс. р.

Составить график проведения работ, определить критический путь и стоимость работ по переоборудованию цеха при нормальном режиме работ.

Провести «сжатие» работ, определить, через какое время после начала выпуска тары фирма может вернуть кредит банку, и минимальную суммарную стоимость работ.

5. Автотранспортному предприятию предстоит освоить новый маршрут между городами А и В. На рисунке представлены различные маршруты следования из А и В, проходящие через несколько других поселков. Расстояния указаны (числами в километрах) около стрелок.

Определить кратчайший маршрут следования автобусов из города А в город В.

6. Пожарной службе необходимо определить кратчайший путь от гаража (пункт А) до нефтеперерабатывающего завода (пункт В) по данным в километрах, указанным на рисунке.

7. Строительной фирме необходимо проложить водопроводные трубы к 9 объектам, на которых она ведёт строительство. Числа не рёбрах указывают длину труб в метрах. Узел 1 – подсоединение к водопроводной трассе (рис.).

Отсутствие ребра между двумя узлами означает, что соединение соответствующих объектов невозможно.

Найти такое соединение узла 1 с объектами строительства, чтобы суммарная длина трубопроводов была минимальной.

Дата добавления: 2014-01-11