Оптимальная стратегия замены оборудования

Динамическое программирование

Динамическое программирование – один из разделов оптимального программирования, в котором процесс принятия и управления может быть разбит на отдельные этапы.

Экономический процесс является управляемым, если можно влиять на ход его развития. Под управлением понимается совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса. Например, выпуск продукции предприятием – управляемый процесс. Совокупность решений, принимаемых в начале года по обеспечению предприятия сырьём, замене оборудования, финансированию и т. д., является управлением. Необходимо организовать выпуск продукции так, чтобы принятые решения на отдельных этапах способствовали получению максимально возможного объёма продукции или прибыли.

Одним из основных методов динамического программирования является метод рекуррентных соотношений, который основывается на использовании принципа оптимальности, разработанного американским математиком Беллманом. Принцип состоит в том, что, каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придёт система в конце данного шага. Использование данного принципа гарантирует, что управление, выбранное на любом шаге, лучше с точки зрения процесса в целом.

В некоторых задачах, решаемых методом динамического программирования, процесс управления разбивается на шаги. При распределении на несколько лет ресурсов деятельности предприятия шагом считается временной период; при распределении средств между предприятиями – номер очередного предприятия.

Одной из важнейших экономических проблем является определение оптимальной стратегии в замене старых станков, агрегатов, машин на новые.

Старение оборудования включает его физический и моральный износ, в результате чего растут производственные затраты по выпуску продукции на старом оборудовании, увеличиваются затраты на ремонт и обслуживание, снижаются производительность и ликвидная стоимость.

Вполне возможно, что старое оборудование выгоднее продать, заменить новым, чем эксплуатировать его; причём его можно заменить новым оборудованием того же вида или новым, более совершенным.

Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены. Критерием оптимальности при этом может служить прибыль от эксплуатации оборудования, которую следует оптимизировать, или суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации.

Будем использовать обозначения:

r(t) – стоимость продукции, производимой за один год на единице оборудования возраста t лет;

u(t) – ежегодные затраты на обслуживание оборудования возраста t лет;

s(t) – остаточная стоимость оборудования возраста t лет;

Р – покупная цена оборудования.

Рассмотрим период N лет, в пределах которого требуется определить оптимальный план замены оборудования.

Обозначим через f_N(t) максимальный доход, получаемый от оборудования возраста t лет за оставшиеся N лет цикла использования оборудования при условии оптимальной стратегии.

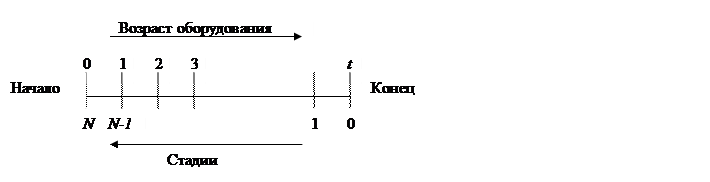
Возраст оборудования отсчитывается в направлении течения процесса. Так, t = 0 соответствует случаю использования нового оборудования. Временные же стадии процесса нумеруются в обратном направлении по отношению к ходу процесса. Например, N = 1 относится к одной временной стадии, остающейся до завершения процесса.

На каждом этапе N -стадийного процесса должно быть принято решение о сохранении или замене оборудования. Выбранный вариант должен обеспечивать получение максимальной прибыли.

Уравнения, помогающие выбрать оптимальное решение, имеют вид:

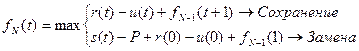
Первое уравнение описывает N -стадийный процесс, а второе – одностадийный. Оба уравнения состоят из двух частей: верхняя строка определяет доход, получаемый при сохранении оборудования; нижняя – доход, получаемый при замене оборудования и продолжении процесса работы на новом оборудовании.

В первом уравнении функция r(t) - u(t) есть разность между стоимостью произведённой продукции и эксплуатационными издержками на N – й стадии процесса.

Функция f_N-1(t+1) характеризует суммарную прибыль от (N - 1) оставшихся стадий для оборудования, возраст которого в начале осуществления этих стадий составляет (t + 1) лет.

Нижняя строка уравнения 1 характеризуется следующим образом: функция s(t) – P представляет чистые издержки по замене оборудования, возраст которого t лет.

Функция r (0) выражает доход, получаемый от нового оборудования возраста 0 лет. Предполагается, что переход от работы на оборудовании возраста t лет к работе на новом оборудовании совершается мгновенно, т. е. период замены старого оборудования и переход на работу на новом оборудовании укладываются в одну и ту же стадию.

Последняя функция f_N-1 (1) в первом уравнении представляет собой доход от оставшихся N – 1 стадий, до начала осуществления которых возраст оборудования составляет один год.

В уравнении для одностадийного процесса нет слагаемого вида f₀ (t + 1), так как N принимает значения 1, 2, …, N. Равенство f₀ (t) = 0 следует из определения функции f_N (t).

Рассмотренные уравнения являются рекуррентными соотношениями, которые позволяют определить величину f_N (t) в зависимости от f_N-1(t+1). Данные уравнения показывают, что при переходе от одной стадии процесса к следующей возраст оборудования увеличивается с t до (t +1) лет, а число оставшихся стадий уменьшается с N до (N – 1).

Уравнения позволяют оценить варианты замены и сохранения оборудования, с тем, чтобы принять тот из них, который предполагает больший доход. Эти соотношения позволяют выбрать линию поведения при решении вопроса о сохранении и замене оборудования, а также определить прибыль, получаемую при принятии каждого из этих решений.

Пример. Определить оптимальный цикл замены оборудования при следующих исходных данных: Р = 10, S(t) = 0, f(t) = r(t) - u(t), представленных в таблице.

t

f(t)

РЕШЕНИЕ. Запишем уравнения в следующем виде:

.

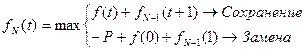
Для N=1

…………………………………………………

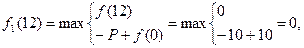
Для N=2

…………………………………………………

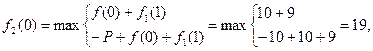
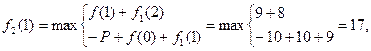
Вычисления продолжаются до тех пор, пока не будет выполнено условие f₁ (1) > f ₂(2), т. е. в данный момент оборудование необходимо заменить, так как величина прибыли, получаемая в результате замены оборудования, больше, чем в случае использования старого. Результаты расчётов помещаются в таблицу, момент замены отмечается звёздочкой, после чего дальнейшие вычисления по строке прекращаются.

t fN(t)

N

N- 1

f1(t)

f2(t)

9*

f3(t)

17^*

f4(t)

24*

f5(t)

30*

f6(t)

35*

f7(t)

41*

f8(t)

48*

f9(t)

54*

f10(t)

60*

f11(t)

65*

f12(t)

72*

По результатам вычислений и по линии, разграничивающей области решений сохранения и замены оборудования, находим оптимальный цикл замены оборудования. Для данной задачи он составляет 4 года.

Ответ. Для получения максимальной прибыли от использования оборудования в двенадцатиэтапном процессе оптимальный цикл состоит в замене оборудования через каждые 4 года.

Задачи для групповой работы на занятии по теме «Динамическое программирование»

1. К началу рассматриваемого периода на предприятии установлено новое оборудование. Зависимость производительности этого оборудования от времени его работы, а также затраты на содержание и ремонт при различном времени его использования приведены в таблице.

Известно, что затраты, связанные с приобретением и установкой нового оборудования составляют 40 млн. р., а заменяемое оборудование списывается. Составить такой план замены оборудования в течение пяти лет, при котором общий доход за данный период времени максимален.

Наименование	Время, в течение которого используется оборудование, годы
Годовой выпуск продукции, млн. р.
Ежегодные затраты на содержание и ремонт оборудования, млн. р.

2. К началу анализируемого периода на предприятии установлено новое оборудование.

Определить оптимальный цикл замены оборудования при следующих исходных данных:

покупная цена оборудования (Р) составляет 12 ден. ед.;

остаточная стоимость оборудования S (t) = 0;

f (t) = r (t) – u (t) – максимальный доход, получаемый от оборудования возраста t лет за год при условии оптимальной стратегии, где r (t) – стоимость продукции, выпускаемой за год на единице оборудования возраста t лет, u (t) – ежегодные затраты на обслуживание оборудования возраста t лет;

N = 8 лет.

Зависимость f (t) от t задана в таблице.

t
f (t)

3. Торговая фирма располагает 5 автолавками, которые могут быть направлены в воскресный день в 3 населённых пункта. Считается, что товарооборот фирмы зависит лишь от количества и ассортимента направляемых товаров и определяется числом посланных в тот или иной населенный пункт машин.

Среднее значение товарооборота в тыс. р. в каждом из населённых пунктов задано в таблице.

Количество автолавок	Товарооборот в населённых пунктах, тыс. р.

Найти оптимальную стратегию фирмы в распределении автолавок по населённым пунктам, максимизирующую общий товарооборот.

4. В таблице указан возможный прирост выпуска продукции четырьмя плодово-консервными заводами в области в млн. р. При осуществлении инвестиций на их модернизацию с дискретностью 50 млн. р., причём на один завод можно осуществить только одну инвестицию.

Составить план распределения инвестиций между заводами области, максимизирующий общий прирост выпуска продукции.

Инвестиции, млн. р.	Прирост выпуска продукции, млн. р.
Заводы

5. В трёх областях необходимо построить 5 предприятий по переработке сельскохозяйственной продукции одинаковой мощности.

Разместить предприятия таким образом, чтобы осуществить минимальные суммарные затраты на их строительство и эксплуатацию.

Функция расходов g_i (x), характеризующая величину затрат на строительство и эксплуатацию в зависимости от количества размещаемых предприятий в i -й области, приведена в таблице.

x
g1 (x) g2 (x) g3 (x)

3. Проложить трубопровод меду двумя пунктами А и В так, чтобы суммарные затраты на его изготовление были минимальные. Исходные данные по затратам в млн. р. Для проведения расчётов представлены на рисунке.

Y (север) В

5 6
4 6
3 5

А Х (восток)

Ответы: 1. Оборудование заменить через 3 года.

2. Оборудование заменить через 4 года.

3. В первый населённый пункт направить 1 автолавку, во второй – 3, в третий – 1, при этом товарооборот будет максимальный, равный 64 тыс. р.

4. Инвестировать третьему заводу 50 млн. р., четвёртому заводу – 150 млн. р., максимальный прирост выпуска продукции составит 146 млн. р.

5. В первой области построить 2 предприятия, в третьей – 3, минимальные затраты составят 29 млн. р.

6. 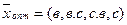, минимальные затраты равны 35 млн. р.

Дата добавления: 2014-01-11