Основные показатели динамики экономических явлений

Требования, предъявляемые к временным рядам

1. Основным из условий, необходимых для правильного отражения временным рядом процесса, является сопоставимость его уровней. К несопоставимости приводит изменение состава изучаемой совокупности, переход к другим единицам измерения, изменение методологии учета и расчета показателей, инфляционные процессы и т.п. Временные ряды являются несопоставимыми и в том случае, когда показатели относятся к различным периодам года или приведены на разные даты. При обнаружении несопоставимости уровней ряда должна применяться процедура смыкания рядов.

2. Некоторые методы анализа и прогнозирования предъявляют достаточно "жесткие" требования к длине ряда, поэтому иногда вместо годовых данных желательно взять поквартальные или помесячные. Так, для успешного изучения сезонных колебаний на базе квартальных или помесячных данных желательно иметь информацию не менее чем за 3 года.

Применение математического аппарата также накладывает ограничение на допустимую длину временных рядов при использовании их в регрессионном анализе. Для такого анализа нужно иметь временные ряды, длина которых в несколько раз (не менее чем в 4-6 раз) превосходит количество независимых переменных в уравнении регрессии.

3. Для анализа динамики явления необходимо, чтобы информация была полной, т.е. временные ряды не должны иметь пропущенных значений, которые могут объясняться как недостатком при сборе информации, так и произошедшими изменениями в системе отчетности.

4. Важным этапом при построении качественных прогнозных моделей является выявление во временном ряду аномальных (нехарактерных) значений. Обычно аномальные значения можно обнаружить визуально, при помощи графического представления временных рядов.

Соответствие исходной информации всем указанным требованиям проверяется на этапе предварительного анализа временных рядов. Лишь после этого переходят к расчету и анализу основных показателей динамики, построению моделей, получению прогнозных оценок.

Закономерности выявляются с помощью показателей динамики, формулы которых представлены в таблице. Все эти показатели могут быть рассчитаны либо базисным, либо цепным способом. В основе расчета лежит сравнение уровней временного ряда. Если сравнение осуществляется с одним и тем же показателем (y_б), принятым за базу сравнения, то показатели называются базисными (во временных рядах часто за базу сравнения берется первый уровень ряда y₁). Если каждый уровень (y_t) сравнивается с предыдущим (y_{t- 1}), то вычисленные показатели называются цепными.

Показатель динамики	Способ расчета
базисный	цепной
Абсолютный прирост
Темп роста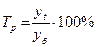
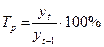
Темп прироста

Абсолютный прирост определяется как разность двух сравниваемых уровней и показывает скорость изменения уровней ряда. Если цепные абсолютные приросты со временем возрастают, то исследуемое явление развивается с ускорением. Ускорение абсолютного прироста – это разность между абсолютными приростами, вычисленными цепным способом. Абсолютное ускорение позволяет увидеть, насколько данная скорость (абсолютный прирост) больше или меньше предыдущей.

Темп роста характеризует отношение двух сравниваемых уровней ряда, выраженное в процентах. Показатели, выраженные в коэффициентах, принято называть коэффициентами роста. Цепные темпы роста характеризуют интенсивность изменения уровней от года к году, базисные – фиксируют интенсивность роста (снижения) за весь интервал времени между текущими и базисными уровнями.

Темп прироста характеризует абсолютный прирост в относительных величинах. Определенный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения.

Если систематически растут цепные темпы роста или прироста, то ряд развивается с относительным ускорением, которое можно определить как разность следующих друг за другом темпов роста или прироста. Полученная величина выражается в процентных пунктах (п.п.).

Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за этот же промежуток времени или как сотую часть уровня предыдущего периода.

Для получения обобщающих показателей динамики развития определяются средние величины: средний абсолютный прирост, средние темпы роста и прироста. Величина среднего абсолютного прироста показывает скорость развития явления за изучаемый интервал времени и вычисляется по формуле:

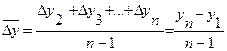
где n - длина временного ряда.

Для определения средней скорости изменения явления за рассматриваемый период времени вычисляют средний темп роста. Этот показатель рассчитывают по формуле средней геометрической:

Средний темп прироста соответственно равен:

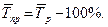
К расчету среднего уровня чаще всего прибегают для рядов, изменение которых стабилизируется в течение большого периода времени (например, средний уровень урожайности за ряд лет), а также для рядов с колеблющимися уровнями за короткие промежутки времени (например, численность работников предприятий изменяется каждый день и поэтому для отражения работы предприятия рассчитывается показатель средней численности работников).

Средний уровень интервального ряда с равностоящими уровнями определяется по формуле средней арифметической:

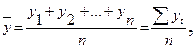
Средний уровень моментного ряда с равностоящими уровнями определяется по формуле средней хронологической:

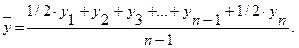
Если определяются средние уровни для рядов с неравностоящими уровнями, то используются формулы взвешенных средних величин.

Дата добавления: 2014-01-20