Компоненты временного ряда. Виды тенденций и методы их определения

Уровни временного ряда со временем меняются, колеблются, эта колеблемость не одинакова и может быть вызвана влиянием различного рода факторов. Принято выделять 4 типа таких факторов:

1) долговременные, формирующие общее направление развития (тенденцию) в изменении анализируемого явления. Обычно эта тенденция описывается с помощью той или иной функцией, которая называется функцией тренда;

2) сезонные, формирующие периодически повторяющиеся в определенное время года колебания анализируемого явления;

3) циклические, формирующие изменения изучаемого явления, обусловленные действием долговременных циклов. Циклические изменения похожи на сезонные тем, что они являются повторяющимися и волнообразными, но отличаются большей длительностью циклов. Циклические колебания в экономических процессах примерно соответствуют циклам конъюнктуры;

4) нерегулярные, не поддающиеся учету и регистрации факторы, которые для социально-экономических явлений делятся на 2 группы:

а) внезапные, приводящие к скачкообразным структурным изменениям в изучаемом процессе (например: война, эпидемия);

б) случайные, являющиеся результатом действия большого количества относительно слабых второстепенных факторов.

В зависимости от того, как взаимосвязаны факторы между собой, выделяют следующие структурные схемы формирования значений ряда:

Y_t = F_t+S_t+C_t+E_t - аддитивная схема;

Y_t = F _t · S _t ·C _t ·E _t - мультипликативная схема;

Y_t=F_t ·S_t ·C_t+E_t - смешанная схема,

где F _t – трендовая компонента, S _t - сезонная компонента, C _t - циклическая компонента, E _t - случайная компонента.

Во всех случаях во временных рядах предполагается непременное участие случайного компонента. Примером временного ряда, не содержащего основную тенденцию и периодические составляющие(т.е. когда Y_t = E_t), может служить ряд

Компоненты временных рядов, имеющих в своем развитии периодические колебания, наслаивающихся на тренд, могут иметь аддитивный или мультипликативный тип связи. Отличительная особенность аддитивной модели заключается в том, что характер периодических колебаний, т.е. амплитуда этих колебаний не изменяется во времени.

При мультипликативном типе связи амплитуда колебаний растет с увеличением среднего значения ряда, и наоборот амплитуда колебаний уменьшается при снижающейся тенденции.

Временной ряд с явно выраженной тенденцией к снижению

Во временных рядах, описывающие социально-экономические процессы могут наблюдаться тенденции трех видов: тенденция среднего уровня, тенденция дисперсии и тенденция автокорреляции.

Под тенденцией среднего уровня (основной тенденцией) понимают некоторое общее направление развития явления. Обычно основную тенденцию можно представить графически более или менее гладкой траекторией. Предполагается, что такая траектория, которую можно охарактеризовать в виде некоторой математической функции времени, характеризует основную закономерность развития во времени и в некоторой мере свободна от случайных воздействий. Эту функцию принято называть трендом.

Тенденция дисперсии представляет собой тенденцию изменения отклонений между фактическими уровнями и расчетными уровнями, найденными по математической формуле тренда. Этот вид тенденции легко представить графически.

Тенденцией автокорреляции является тенденция изменения связи между отдельными уровнями временного ряда.

Часто во временных рядах с незначительной тенденцией развития во времени и существенной колеблемостью уровней не всегда удается определить: присутствует ли тренд в данном ряду или нет.

Основные подходы к решению этой задачи основаны на проверке гипотезы о неизменности среднего уровня временного ряда. Для решения этой задачи используются критерии, отличающиеся друг от друга, как мощностью, так и сложностью математического аппарата: метод проверки разностей средних уровней; метод фостера-стюарт; критерий «восходящих и нисходящих» серий; критерий серий, основанный на медиане выборки и другие.

На практике чаще всего используют метод Фостера-Стюарта, который позволяет обнаружить как тенденцию среднего уровня, так и тенденцию дисперсии. Этот метод можно реализовать в виде следующей последовательности шагов:

1. Каждый уровень ряда, начиная со второго, сравнивается со всеми предыдущими, при этом определяются значения вспомогательных характеристик u_t и m _t (т.е. u _t = 1,если y_t больше всех предшествующих уровней, а m_t = 1, если y_t меньше всех предшествующих уровней).

2. Вычисляются значения s _t = u_t + m_t и d_t = u_t - m_t для всех t = 2, 3,..., n.

3. Находятся характеристики, где показатель S применяется для обнаружения тенденции дисперсии, а показатель D - для обнаружения тенденции среднего уровня.

4. После того, как для исследуемого ряда найдены фактические значения S и D, определяются расчетные значения критерия t_D и t_S: 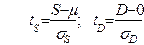, где m - математическое ожидание величины S, определяемое для случайного распределения уровней во времени,

s_S - среднеквадратическая ошибка величины S,

s_D - среднеквадратическая ошибка величины D.

5. Расчетные значения t_D и t_s сравниваются с критическим t_a, взятым из таблицы t -распределения Стьюдента для определенного уровня значимости a. Если расчетное значение t_D больше критического t_a, тогда гипотеза об отсутствии тенденции среднего уровня или дисперсии отвергается Если расчетные значения меньше критического значения t_a,, тогда гипотеза об отсутствии тенденции во временном ряду подтверждается.

Дата добавления: 2014-01-20