Типы уравнений в частных производных

Эволюционные уравнения в физике. Численные методы решения эволюционных уравнений.

Эволюционные уравнения - уравнения, описывающие процессы, протекающие во времени (распространение тепла, распространение волн).

Многие прикладные и теоретические задачи приводят к диф.уравнениям. Исследование задачи может считаться законченным только после того, как это уравнения решены.

В некоторых случаях можно указать формулу. Однако, не всегда это удается. Тогда прибегают к так называемым модельным методам и методам численного решения диф.уравнений.

Название некоторых из таких методов- метод Ньютона, Эйлера, Лобачевского, Чебышева, Гаусса, Эрмита и т.д.

При исследовании эволюционных задач используются энергетические неравенства, спектральные признаки, принцип максимума и др.

Многие задачи физики сводятся к интегрированию уравнений в частных производных. Эти уравнения возникают при моделировании физических полей:

эл/м, температурных, гидродинамики и т.д.

Многие задачи физики сводятся к интегрированию уравнений в частных производных.

Диф. уравнение с частными производными r-го порядка, называется квазилинейным, если оно линейно относительно производных r-го порядка от неизвестной функции Ф.

Рассмотрим квазилинейные уравнения с частными производными 2 порядка с двумя независимыми переменными.

(1)

где a_i, B- заданные непрерывно дифференцируемые функции от 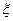, , 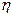, , 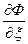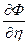Ф.

a² ₁₂ – a₁₁a₂₂=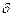- дискриминант уравнения (1).

1) Если a₁₁a₂₂-a₁₂²<0 - уравнение (1) гиперболического типа.

2) Если a₁₁a₂₂-a₁₂²=0 - уравнение (1) параболического типа.

3) Если a₁₁a₂₂-a₁₂²>0 - уравнение (1) эллиптического типа.

Примеры:

Уравнение теплопроводности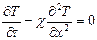

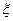(= t, 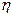= x), a₁₁ = a₁₂ = 0, a₂₂ = - 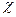, a₁₁a₂₂ = 0 – параболическое.

Волновое уравнение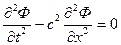

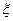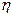(= t², = x² ), a₁₁ = 1, a₁₂ = 0, a₂₂ = - c², a₁₁a₂₂ < 0 - гиперболическое.

Уравнение Пуассона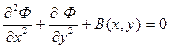

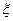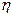(= t², = x²), a₁₁ = 1, a₁₂ = 0, a₂₂ = 1, a₁₁a₂₂ > 0 - эллиптическое.

Дата добавления: 2014-01-20