Реализация неявной схемы

Неявную схему рассчитываем итерациями. Простые итерации сходятся медленно, запас устойчивости для их сходимости невелик, поэтому чаще всего используется итерационная процедура Ньютона. Суть этой процедуры:

Присваиваем неизвестной величине Т ⁿ⁺¹индекс итерации k.

Нелинейное относительно неизвестных Т ⁿ⁺¹слагаемые в правой части уравнения:

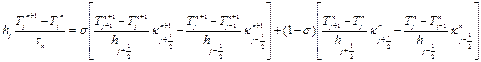Раскладываем в ряд по малому параметру:

,

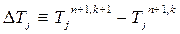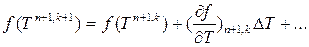
Ограничиваемся линейными членами разложения. Имеем:

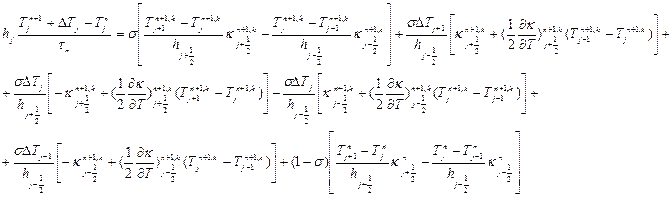
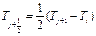Система (6 ) трехдиагональна относительно неизвестных 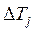и вычисляется методом прогонки. В качестве Т ^{n+1, 0}обычно используют Т ⁿ. Для получения хорошей точности (4-6 знаков) достаточно 3-5итераций. Все затраты машинного времени на реализацию трехдиагональной схемы с лихвой окупаются возможностью увеличения 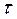и гарантированной устойчивостью счета.

10.Перенос примесей в приземном слое атмосферы. Сложность исследования динамики распространения пассивных(не испытывающих превращений) примесей связана с многомерностью, неоднородностью и нестационарностью изучаемых систем. Неоднородность системы, которая обусловлена зависимостью различных параметров атмосферы (ветра 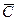, коэффициентов турбулентной диффузии 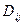, температуры и т. д.) в первую очередь от вертикальной z-компоненты, является дополнительным усложняющим фактором. Возможная нестационарность обусловлена флуктуациями ветра и временной зависимостью функции источников Q(r,t). На процесс распространения примесей в атмосфере оказывают влияние множество факторов, но основными являются два: ветровой снос и диффузионное расплывание. Эти два физически эффекта можно учесть в рамках математической модели, в основе которой лежит квазилинейное д.у. в частных производных:

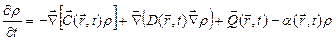(1),где t – время, 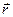-радиус-вектор, 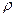-плотность примеси, 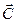- вектор скорости ветра, 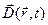-тензор турбулентной диффузии, Q(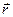,t) – совокупность источников и стоков рассматриваемой примеси, a - параметр, описывающий “вымывание” примеси из атмосферы за счёт различных факторов. Источники загрязнения определяются функцией Q, которая определяет временную динамику выбросов и их параметры. Уравнение (1) записано в векторной форме. Для решения задачи распространения примеси в приземном слое атмосферы удобно работать в декартовой системе координат: x и y – координаты в плоскости поверхности земли, а z – вертикальная координата. Слагаемое 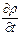описывает изменение концентрации примесей со временем в точке с координатами (x,y,z). Диффузионный перенос Величины 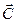и 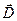являются эмпирическими параметрами, учитывающими как состояние атмосферы, так и рельеф местности. Можно считать, что коэффициент диффузии 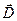на небольших высотах линейным образом зависит от величины скорости ветра, не обращаясь в нуль при 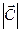=0. Поэтому в нашей модели принято 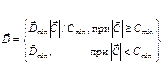В тропосфере коэффициент турбулентной диффузии составляет 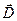=3*10⁵ (см²/с). В зоне перемешивания для коэффициента диффузии: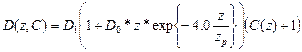,здесь D(z,C)=D₁(C(0)+1) – коэффициент диффузии у земли; z_p-высота пограничного слоя. Ветровой перенос. Первое слагаемое справа в (1) обусловлено ветром в плоскости земли 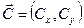: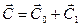,где необходимо учитывать нарду с постоянной составляющей 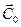и флуктуирующую часть 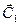. Среднее направление ветра в каждой точке плоскости (x,y) характеризуется углом j₀ между осью x и направлением ветра, а дисперсия направлений задаётся параметром s_j. Тогда при нормальном распределении направлений ветра 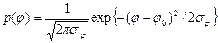.Вычисление истинного направления в каждый момент времени можно легко смоделировать с помощью стандартного алгоритма генерации случайных чисел. 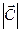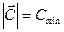Аналогичным образом моделируются и флуктуации величины - скорости ветра.В случае отсутствия ветра и при очень слабом ветре мы полагаем, что , а направление ветра произвольно. Зависимость скорости ветра от вертикальной координаты выбираем в виде: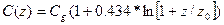,где величина С_g – характеризует скорость ветра у поверхности земли, параметр z₀ определяет шероховатость поверхности. Модель источников и стоков. К исходным данным для проведения расчётов по данной методике необходимо знание источников загрязнения – координаты, высота, химический состав и объём выбросов.Высота выброса примеси в атмосферу, дальнейшее её рассеяние и осаждение зависят не только от высоты источника, но и от таких параметров примеси, как температура и скорость её вытекания из трубы. Пусть труба имеет высоту Н₀, её радиус на выходе примеси – R₀, скорость выноса из жерла трубы - w₀, температура атмосферы Т_а и температура примеси - Т_а+DT. Тогда эффективная добавка DН к высоте трубы Н₀ (Н = Н₀ + DН) удовлетворительно аппроксимируется соотношением: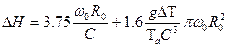.Здесь первый член описывает вертикальную инерцию примеси, а второй - её дополнительную “архимедову” плавучесть.Выброшенная из трубы примесь попадает в приземной слой на некотором удалении от трубы, величина которого зависит от силы и направления ветра, высоты трубы и толщины пограничного приземного слоя атмосферы, коэффициента диффузии и других параметров задачи. При этом примесь успевает продиффундировать поперёк направления ветра.

Для описания этих эффектов введём в плоскости (x,y) систему декартовых координат (x,h), начало которой локализовано на источнике примеси, а ось x направлена по ветру. По поперечной к направлению ветра координате h имеет место диффузия, которая за время t(x)=x/C превращает начальное “точечное ” распределение Q = Q₀*d(x)*d(h) (d-дельта-функция Дирака) в нормальное по h:.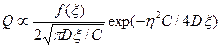

Такой же процесс диффузии имеется и вдоль направления ветра. Однако из-за неоднородности по высоте ветрового сноса распределение по координате x будет существенно отличаться от нормального. Удовлетворительная точность достигается при следующей аппроксимации:

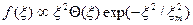,где Q(x) – функция Хевисайда. Нормировка распределений приводит к результату: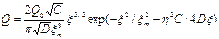,где Q₀- мощность источника.Величину x_m с учётом зависимости C и D от вертикальной координаты z в приземном слое атмосферы можно представить в виде: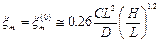,где L – толщина приземного слоя атмосферы.

Если рассматриваемая примесь не газообразная и её частицы не обладают “плавучестью” то следует учесть эффект ускоренного выпадения этой примеси на землю. Вводя для этого стоксову скорость падения отдельной частицы w₁, имеем:.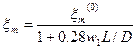

Достаточно крупный туман или дождь очищает атмосферу, осаждая примесь на землю. Этот эффект можно учесть модельно с помощью введённого в (1) параметра a. Соответствующий вклад в параметр a пропорционален кинематической вязкости воздуха v и обратно пропорционален квадрату размера капли тумана r_m.В зависимости от величины и знака вертикального градиента температуры, исходящая из локализованных и распределённых источников примесь может либо ”всплыть” в верхние слои атмосферы, либо прижиматься к земле и накапливаться в приземном слое толщиной порядка высоты деревьев и зданий. И в первом, и во втором случаях соответствующие эффекты можно описать с помощью модельного параметра a. Однако второй из указанных факторов необходимо учесть с помощью локального уравнения “накопления”:

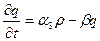,где q – локальная плотность накапливающейся в приземном слое атмосферы примеси; b - параметр, описывающий полное “вымывание” накопленной примеси. Влияние температурной устойчивости атмосферы на турбулентный обмен оценивается по безразмерной величине b, характеризующей отношение разности температур на выбранных уровнях к скорости ветра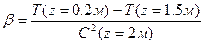

12.Уравнение Лапласа, Пуассона, Гельмгольца в ортогональных системах координат.Краевые условия для эллиптических уравнений. Уравнением эллиптического типа называется квазилинейное Д.У. в частных производных второго порядка с двумя независимыми переменными:

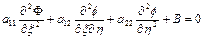, где 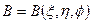, , 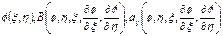если 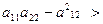0.

Уравнения Лапласа и Пуассона возникают при моделировании стационарных физических полей. 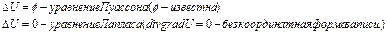Общее решение этих уравнений представимо в виде:U=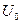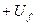Известно, что Д.У. в частных производных имеет ∞ множество решений. Типичным дополнительным условием, обеспечивающим единственность решения Д.У в частных производных является краевое условие, определяющее поведение исходных функций на границе области.Оператор ∆ в ортогональных системах координат:

Д.С.К: , Ц.С.К: 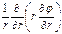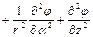,С.С.К:,

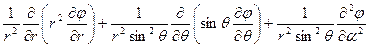Волновое уравнение, переписанное через метод комплексных амплитуд, называется уравнением Гельмгольца:

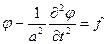∆-волновое уравнение.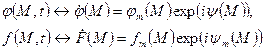

Следовательно уравнение Гельмгольца будет иметь вид: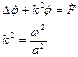Здесь 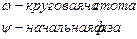Существует несколько типов краевых задач. Рассмотрим их на примере уравнения Лапласа. 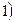Первая краевая задача-задача Дирихле: найти гармоническую в области функцию по её значениям на границе этой области.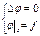 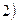Вторая краевая задача-задача Неймана: найти гармоническую в области функцию по значениям её нормальной производной на границе: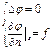,s-поверхность, n-нормаль к этой поверхности.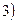Третья краевая задача: найти гармоническую в области функцию по значениям линейной комбинации функции и её нормальной производной на границе.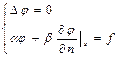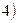Смешанная краевая задача: отыскать гармоническую функцию, если на части границы задана сама функция, а на другой, её дополняющей части, задана нормальная производная. 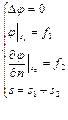Совершенно аналогично ставятся краевые задачи для эллиптических уравнений для внешних областей. В этом случае необходимо указать поведение искомой функции на бесконечности.

Дата добавления: 2014-01-20