Одномерные волны. Формула Даламбера

Р/м колебания струны во всем пр-ве. Такие колебания описываются задачей Коши:

/ ∂²u/∂x²-1/a² ∂²u/∂t²=0

| u(x,0)=ψ₀(x) (*)

∂u/∂t (x,0)=ψ₁(x)

Решение этой задачи можно записать в виде: u(x,t)=φ₁(x-at)+φ₂(x+at) (**), φ₁ и φ₂ - " диф-мые по x и по t ф-ции. φ₁ описывает движение против оси x, а φ₂ – вдоль.Построим решение поставленной задачи Коши (*) для волнового ур-я. Вид φ₁ и φ₂ определим из начальных условий задачи:

ψ₀=φ₁(x)+φ₂(x), ψ₁=-aφ^’₁(x)+aφ^’₂(x). Проинтегрировав второе уравнение, получим:φ₁+φ₂=1/a _x0∫^xψ₁(x)dx+c, c - " константаСкладывая и вычитая первое и третье ур-я, получим:φ₁=-1/2a _x0∫^xψ₁(x)dx-c/2+ψ₀(x)/2, φ₂=1/2a _x0∫^xψ₁(x)dx+c/2+ψ₀(x)/2Подставляя эти уравнения в (**), получим решение задачи коши для волн ур-я:u(x,t)=(ψ₀(x-at)+ψ₀(x+at))/2+1/2a _x-at∫^x+atψ₁(x)dx – ф-ла Даламбера

17. Сферические волны. Формула Пуассона. Найдем общий вид сферич симметр решения 3-х мерн волн уравн. Запишем в сферич коорд. 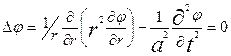(1)или(2) или 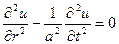(3) для u(r,t)=rφ(r,t) (4)

общее решение в виде 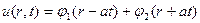(5) (6) cферич симметр решение волнового ур-я. 1-е слогаемое справа опис падающую волну распростр от т. r=0 в ∞ с затуханием 1/r. 2-е слогаемое опис. Отражённую сферич волну движ к т. r=0 с возрастанием амплитуды: 1/r. Построим решение след задачи Коши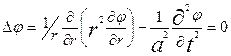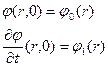будем искать огранич в т. r=0 решение 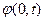<∞ переходя к вспомогат зад для u получим зад Коши для полуогранич. струны с закреплён концами 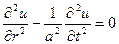, 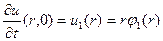0<r<=∞

Дата добавления: 2014-01-20