Численная реализация метода установления для уравнения Пуассона. Устойчивость и скорость сходимости

Рассмотрим особенности численного решения эллиптического уравнения на примере уравнения Пуассона. Для удобства ограничимся двумерной задачей Дирихле в квадратной области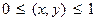

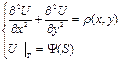
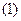где S – длина дуги, отсчитываемая вдоль границы 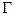, 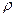и 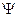- заданные функции.Введем квадратную сетку 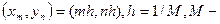целое число. Запишем конечно-разностный аналог уравнения (1), заменяя вторые производные стандартной трёхточечной аппроксимацией: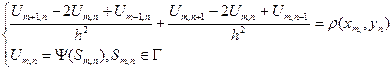Схема (2) есть СЛАУ относительно 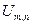Решить систему (2) каким либо общим методом численной линейной алгебры (метод Гаусса) невыгодно, т.к. такой метод не учитывает сильную разреженность матрицы системы (2) (действительно, из общего числа 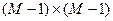неизвестных только 5 содержаться в каждом из уравнений (2)) и поэтому оказывается чересчур медленным. Вместо этого используются специальные методы: прямые или итерационные. Итерационные методы менее быстрые, чем прямые, но за то более универсальны, т.к. не зависят от геометрии расчетной области и легче программируются.В данном случае рассматривается итерационный подход, эквивалентный расчету на установление развивающегося во времени процесса. Рассмотрим вспомогательную нестационарную залачу:

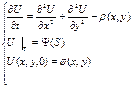
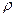где и 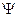- те же самые, что и в (1), а 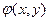- произвольно. Решение задачи (3) при 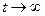стремится к равновесному распределению 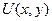, опнсываемому задачей (1), В соответствии с этим вместо (1) будем решать (3), а вместо равновесной схемы введем схему:

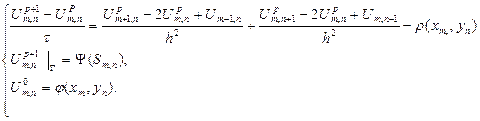
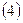Вычисление 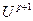по уже известным 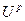в данной схеме (4) не составляет труда. Можно показать, что наибольшая сходимость достигается в случая: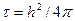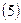Схема (4) с выбором оптимального “временного шага” согласно (5) называется схемой Якоби и является простейшей из итерационных схем.Для квадратной области число итераций, необходимых для достижения заданной точности при равно: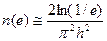Сходимость итераций по схеме (4)-(5)имеет место и в случае расчетной области произвольной сложной формы. Схема (4) выдерживает обобщение на случай задачи Дирихле с переменными коэффициентами.

15. Волновое ур-е. Начал и краевые усл-я для волнового ур-я. Волновое уравнение можно записать в таком виде:∆φ-1/a² ∂²φ/∂t²=f(M,t), a определяет скорость распространения волны,или спользуя оператор Даламбера:□φ=f(M,t), □ – даламбериан

Волн ур-е имеет ∞ мн-во решений. Заданием краев и начал усл выделяется конкретное реш-е. Краевые усл-я для волн ур-я ставятся также как и для ур-я Лапласа. Начал усл заключаются в задании распределения ф-ции и ее перв производной и имеют вид: / φ(M,0)=f₁(M) ∂φ/∂t (M,0)=f₂(M)Совок волн ур-я, краевых и начал усл отражает начально-краевую задачу для волн ур-я.

Дата добавления: 2014-01-20