Предел функции

1. Предел функции в точке.

Односторонние пределы.

Пример.

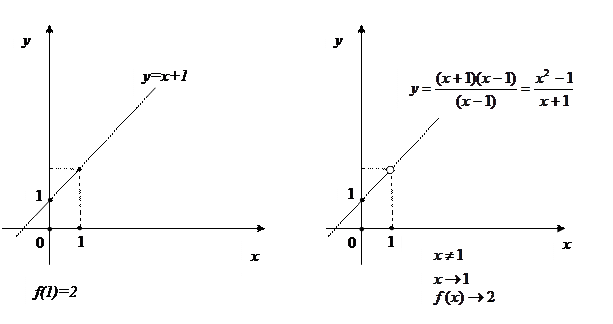
Пусть функция y=f(x) задана в некоторой окрестности точки 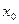, за исключением, быть может, самой точки .

Опр. 1. Точка А называется пределом функции y=f(x) при , если для любой последовательности точек 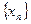, сходящейся к 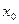, последовательность значений функции 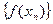сходится к А. В этом случае пишут: 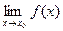= А, ил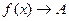и при .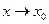

Это определение называют определением предела по Гейне (нем. математик XIX в.)

Замечание. Если точка 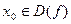, то предел 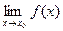, если он существует, равен значению функции в данной точке 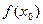. (См. рис.1)

Опр. 2. Если при стремлении к 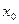x принимает лишь значения, меньшие (большие) 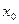, и при этом 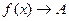, то говорят об одностороннем пределе слева 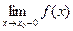(справа ).

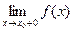Пример.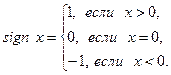

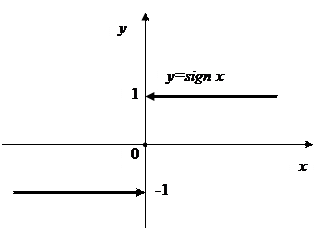
Утверждение. Предел функции в точке существует тогда и только тогда, когда существуют и равны оба односторонних предела функции в данной точке.

Существует и другое (равносильное) определение предела функции, в котором используется понятие окрестности. Оно называется определением по Коши.

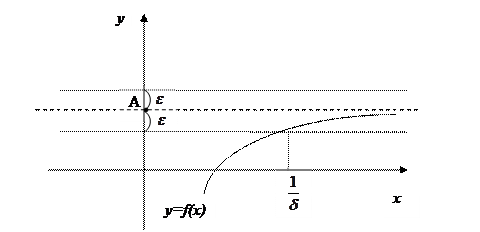
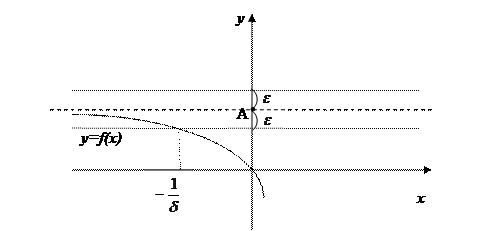
Опр. 3. Число А называется пределом функции y=f(x) при 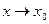, если для любого, даже сколь угодно малого положительного числа 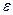, найдется такое положительное число 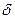, зависящее от 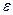, что для всех x, удовлетворяющих условию 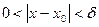, верно неравенство .

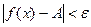В символической форме это определение записывается так:

.

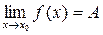
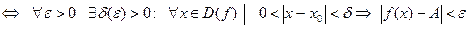Вопрос. Где здесь окрестности? Раскрыть скобки в неравенствах.

Опр.3 можно также сформулировать в следующем общем виде:

Число А называют пределом функции y=f(x) при 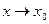и пишут 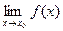= А, если .

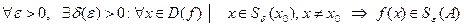Геометрический смысл данного определения 3 заключается в следующем: какую бы (даже сколь угодно малую) окрестность точки А на оси Оу мы ни взяли, всегда найдется окрестность точки 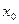на оси Ох, являющаяся ее прообразом.

2. Бесконечные пределы.

Общее определение предела позволяет дать определение и для случаев, когда 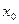или А являются несобственными точками, т.е. .

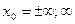Опр. 4. Число А называют пределом функции y=f(x) при 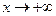и пишут 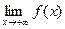= А, если:

.

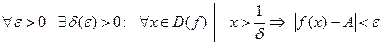Опр. 5. Число А называют пределом функции y=f(x) при и пишут 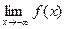= А, если:

.

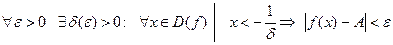Самостоятельно: сформулировать определение предела при .

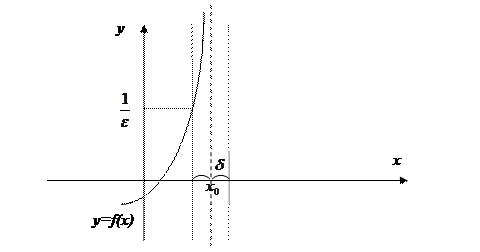
Опр.6. Говорят, что функция y=f(x) имеет предел при , равный и пишут 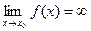, если:

.

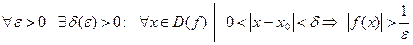Самостоятельно: сформулировать определение предела, равного.

3. Бесконечно малые и бесконечно большие функции, их связь.

Опр. Функция 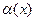называется бесконечно малой при 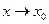функцией, если ее предел при 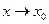равен нулю:

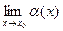=0 .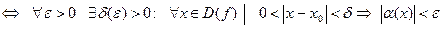

Опр. Функция 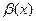называется бесконечно большой при 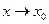функцией, если ее предел при 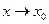есть несобственное число:

=.

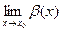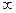
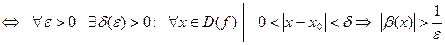Пример. Функция 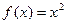является: БМ при 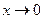; ББ при 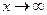; не является ни БМ, ни ББ при .

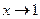Теорема 1. (о связи предела и бесконечно малой функции). Если функция

y=f(x) имеет предел 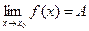, то разность между функцией и значением ее предела есть бесконечно малая при .

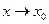Док-во. Имеем:

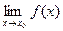= А .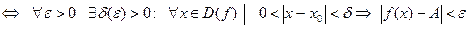

Надо доказать, что 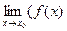- А)=0, т.е.

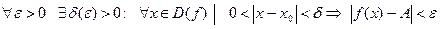. Очевидно, что это условие выполнено. ▲

Следствие. Если функция y=f(x) имеет предел , то ее можно представить в виде суммы этого числа А и бесконечно малой при функции : .

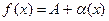Теорема 2 (о связи БМ и ББ функций). Если 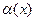есть БМФ, и в некоторой окрестности точки 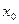, то функция есть ББ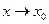Ф. Если 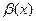есть ББ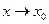Ф, то функция 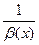есть БМ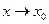Ф.

Доказать самостоятельно, используя определение предела.

4. Свойства бесконечно больших и бесконечно малых функций.

Дата добавления: 2014-01-20