
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кольца и поля
|
|
|
|
Множество R с бинарными операциями + и × называется кольцом, если:
1) R – абелева группа относительно операции +;
2) операция умножения ассоциативна;
3) выполнены законы дистрибутивности, то есть для всех a, b, c Î R
a ×(b + c)= a × b + a × c,(b + c)× a = b × a + c × a.
Нейтральный элемент аддитивной группы кольца называется нулём кольца (обозначается 0). Обратный элемент к a по сложению обозначается (- a).
Кольцо называется кольцом с единицей, если оно имеет мультипликативную единицу, то есть такой элемент e, что a × e = e × a = a для любого a Î R. Кольцо называется коммутативным, если операция умножения коммутативна.
Подкольцо кольца R - это подмножество R ¢, являющееся кольцом, обозначается R ¢£ R.
Пример 3. Кольца:
а) множество целых чисел Z, множество четных чисел - подкольцо;
б) множество рациональных чисел Q;
в) множество действительных чисел R;
г) множество {0,1}, в котором сложение и умножение задано таблицами:
| + | × | |||||
Коммутативное кольцо называется полем,если его ненулевые элементы образуют группу относительно операции умножения. Иначе говоря, полем называется множество Р элементов, на котором определены операции сложения + и умножения ×, обладающие свойствами коммутативности, ассоциативности и дистрибутивности, при этом относительно обеих операций существуют нейтральные элементы и для всякого a (для всякого b ¹0) существует обратный элемент относительно операции + (относительно операции ×). Так как поле Р содержит 1, то МР (п) - кольцо с единицей Е матриц порядка п над Р.
Поле, состоящее из конечного числа элементов, называется конечным.
Пример 1.4. Поля:
а) множество рациональных чисел;
б) множество действительных чисел;
в) множество комплексных чисел;
г) множество {0,1}, рассмотренное в примере 3г. w
4. Кольца матриц
Важное место при изучении математических моделей занимают матрицы. Матрицей А размера п ´ т над множеством X называется прямоугольная таблица с п строками и с т столбцами, в каждой ячейке которой записан элемент множества X. Обозначается: А =(аij), где аij есть элемент матрицы А, записанный в i –й строке и j –м столбце, i= 1,…, n, j =1,…, m. Если п = т, то А – квадратная матрица порядка п.
Для матриц над произвольным кольцом R определено сложение и умножение. Если А= (аij), В= (bij) - матрицы размера п ´ т, то А + В =(cij) – тоже матрица размера п ´ т, где cij = аij + bij. Если А =(аij) - матрица размера п ´ т и В= (bij) - матрица размера т ´ r, то А × В =(cij) - матрица размера п ´ r, где cij = 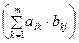 . Сложение и умножение элементов матриц выполняется в R.
. Сложение и умножение элементов матриц выполняется в R.
Главной диагональю квадратной матрицы порядка п называют упорядоченную выборку элементов (a 1,1,…, an , n).
Множество квадратных матриц порядка п над кольцом R образует кольцо (обозначим его МR (п)). Матрица А Î МR (п) называется:
1) верхнетреугольной, если аij = 0 при i > j, где 0 - ноль кольца R;
2) нижнетреугольной, если аij = 0 при i < j;
3) диагональной, если А - и верхнетреугольная, и нижнетреугольная.
При заданных операциях:
1) множество матриц размера п ´ т над аддитивной полугруппой (группой) G образует аддитивную полугруппу (группу), где нейтральный элемент есть матрица, состоящая из нулей полугруппы (группы) G;
2)) МR (п) образует кольцо; если кольцо R с единицей, то и МR (п) - кольцо с единицей E, называемой единичной матрицей, у нее главная диагональ состоит из единиц кольца R, а остальные элементы - нули кольца R.
Для любой матрицы А Î МR (п) выполнено: А × Е = Е × А = А. При п >1 кольцо МR (п) некоммутативное, даже если кольцо R коммутативное.
Для множества матриц МR (п) определена операция t внешнего умножения, t: R ´ МR (п)® МR (п), где t(r,(аij))= r ×(аij)=(rаij) для r Î R.
Матрицы А, В Î МР (п) называются взаимно обратными, если А × В=В × А=Е, при этом матрицу А называют обратной к матрице В (обозначается А=В -1) и наоборот. Матрица А называется обратимой, если у неё имеется обратная матрица. Матрица А Î МР (п) обратима Û её определитель[1] не равен 0, такие матрицы называются невырожденными.
Следовательно, подмножество всех невырожденных матриц из МР (п) образует группу относительно умножения.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1602; Нарушение авторских прав?; Мы поможем в написании вашей работы!