Кольца многочленов и формальных степенных рядов

Канонический многочлен или полином f (x) над кольцом R от одной переменной x - это выражение вида:

f (x)= a ₀+ a ₁× x +…+ a_n × xⁿ,

где x - переменная, либо формальная, либо принимающая значения в кольце R ¢, содержащем кольцо R; a ₀, a ₁,…, a_n Î R и элемент a_n ¹0, т.е. a_n отличен от нуля кольца R. Элементы a ₀, a ₁,…, a_n называются коэффициентами многочлена f (x), в частности, a_n – старшим коэффициентом f (x), a ₀ – свободным членом многочлена f (x). Натуральноечисло n называется степенью многочлена f (x)и обозначаетсяdeg f (x).

Многочлен x^k называется одночленом или мономом степени k ³0, и a_k называется коэффициентом при мономе x^k в многочлене f (x).

Множество многочленов над кольцом R от одной переменной x (обозначим его R [ x ]) образует кольцо относительно следующих операций сложения и умножения. Если g (x)= b ₀+ b ₁× x+b ₂× x ²+…+ b_m×x^m, m £ n, то канонический вид суммы многочленов есть

f (x)+ g (x)=(a ₀+ b ₀)+(a ₁+ b ₁)× x +(a ₂+ b ₂)× x ²+…+(a_n + b_п)× xⁿ,

где b_i =0 для i > m, и канонический вид произведения многочленов есть

f (x)× g (x)= с ₀+ с ₁× x+с ₂× x ²+…+ с_{m + п} ×x^{m + n},

где с_i =для всех i= 0,1,…, m + n. В частности, для a Î R

a × f (x)= aa ₀+ aa ₁× x +…+ aa_n × xⁿ.

Отсюда выполнены свойства:

deg(f (x)+ g (x))£max{deg f (x),deg g (x)}, (1)

deg(f (x)× g (x))=deg f (x)+deg g (x). (2)

Нулем кольца R [ x ] является так называемый нулевой многочлен, у которого все коэффициенты – нули кольца R. Кольцо R [ x ] коммутативное Û кольцо R коммутативное. Кольцо R [ x ] имеет единицу e (x)Û кольцо R имеет единицу e, при этом e (x) есть многочлен, у которого свободный член равен e, а остальные коэффициенты равны нулю кольца R.

Положим 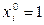для i =1,…, k. Тогда канонический действительный полином или многочлен f (x ₁,…, x_k) над кольцом R от переменных x ₁,…, x_k – это выражение вида:

f (x ₁,…, x_k)=,

где элементы кольца R - действительные числа, называемые коэффициентами многочлена f (x ₁,…, x_k), и только конечное число коэффициентов отлично от нуля кольца R, в частности, a _0…0 – свободный член многочлена f (x ₁,…, x_k). Многочлен 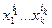называется одночленом или мономом степени r = i ₁+…+ i_k ³0, при этом называется коэффициентом при мономе 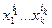в многочлене f (x ₁,…, x_k).

Степенью многочлена f (x ₁,…, x_k) (обозначается deg f (x ₁,…, x_k)) называется максимальная из степеней его мономов с ненулевыми коэффициентами. Данное определение корректно в силу конечного числа слагаемых в формуле.

Множество многочленов над кольцом R от переменных x ₁,…, x_k (обозначим его R [ x ₁,…, x_k ]) образует кольцо относительно операций сложения и умножения.

Если g (x ₁,…, x_k)=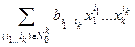, то канонический вид суммы многочленов есть

f (x ₁,…, x_k)+ g (x ₁,…, x_k)= .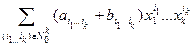

Канонический вид произведения многочленов можно вычислить так:

1) умножить с соответствующими коэффициентами каждый моном многочлена f (x ₁,…, x_k) на каждый моном многочлена g (x ₁,…, x_k), где

=;

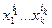
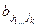
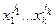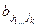
2) записать сумму всех получившихся мономов с коэффициентами и привести подобные мономы (т.е. сумму мономов вида a 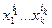+ b 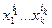+… записать как (a + b +…).

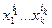Степень суммы и произведения полиномов определена формулами (1.1) и (1.2).

Многочленом будем считать либо канонический многочлен, либо сумму и произведение многочленов, в частности, канонических. Любой многочлен можно привести к каноническому виду. Действительными многочленами называют многочлены над полем действительных чисел.

Дата добавления: 2014-01-20