Корреляционный анализ

Математические методы анализа и прогнозирования

Корреляционный анализ

Введение

2. Регрессионный анализ

3. Факторный анализ

4. Кластерный анализ

5. Анализ динамики и прогнозирования социально-правовых процессов

Заключение

Между социально-экономическими явлениями и процессами воз­можны два вида зависимости: функциональная и стохастическая. При или иных параметров, характеризующих различные явления. Примеры такого рода зависимостей в социальной среде практически не встречаются.

При стохастической (вероятностной) зависимости конкретному значению зависимой переменной соответствует набор значений объ­ясняющей переменной. Это связано, прежде всего, с тем, что на за­висимую переменную оказывает влияние ряд неучтенных факторов. Кроме того, сказываются ошибки измерения переменных: вследствие случайного разброса значений их значения могут быть указаны лишь с определенной вероятностью.

В социально-экономической сфере приходится сталкиваться со многими явлениями, имеющими вероятностную природу. Так, число совершенных и раскрытых преступлений за фиксированный отрезок времени, число дорожно-транспортных происшествий в каком-либо регионе за определенное время - все это случайные величины.

Для изучения стохастических взаимосвязей существуют специальные методы, в частности корреляционный анализ ("корреляция" ­соотношение, связь между имеющимися явлениями и процессами).

Корреляционный анализ - это использование в определенной последовательности совокупности статистических методов обработки ин­формации, позволяющее исследовать взаимосвязи между различными признаками.

Задачей корреляционного анализа как метода математической статистики является установление формы и направления связи, а также измерение тесноты этой связи между изучаемыми случайными признаками.

В статистике величина линейной зависимости между двумя признаками измеряется посредством простого (выборочного) коэффициента корреляции. Величина линейной зависимости одной перемен­ной от нескольких других измеряется коэффициентом множественной ми после устранение части линейной зависимости, обусловленной связью этих переменных с другими переменными.

По форме корреляционные связи могут быть линейными (прямо­линейными) и нелинейными (криволинейными), а по направлению ­

Прямая связь свидетельствует о том, что с увеличением (уменьшением) значений одного признака увеличиваются (уменьшают­ся) значения другого признака. При обратной связи увеличение (уменьшение) значений одного признака ведет к уменьшению (увели­чению) значений другого признака.

Главная задача корреляционного анализа - измерение тесноты связи - решается путем вычисления различных коэффициентов корре­ляции и проверки их значимости.

Коэффициент корреляции может принимать значения при прямой связи от 0 до +1, а при обратной от -1 до 0. При коэффициен­тах, близких к 0, считается, что статистическая линейная связь между признаками отсутствует; при абсолютных значениях коэффици­ентов, меньших 0,3, - связь слабая; при значениях 0,3...0,5 ­связь умеренная; при 0,5...0,7 - связь значительная; при 0,7...0,9 - связь сильная; если значения коэффициентов больше 0,9, то связь считается очень сильной; если коэффициенты равны +1 или -1, то говорится о функциональной связи (что практически не встречается в статистических исследованиях).

Однако такая упрощенная оценка силы связи не всегда кор­ректна, так как степень уверенности в наличии статистической связи зависит от объема исследуемой совокупности. Чем меньше объем совокупности, тем большим должно быть значение коэффициен­та корреляции для принятия гипотезы о существовании зависимости между признаками. С целью количественного измерения степени уве­ренности в существовании линейной статистической связи между признаками введены понятия уровня значимости и пороговых (крити­ческих) значений коэффициента корреляции.

Проверка значимости полученного коэффициента корреляции состоит в сравнении расчетного значения с критическим. При дан­ном числе измерений и задаваемом уровне значимости находится критическое значение, которое сравнивается с расчетным. Если расчетное больше критического, то связь значима, если меньше, то связь или отсутствует (а такое значение коэффициента корреляции объясняется случайными отклонениями), или выборка мала для ее выявления.

Для определения существования и величины линейной зависи­мости между двумя переменными X и Y необходимо осуществить две процедуры. Первая заключается в графическом отображении точек [{Xi,Yi},i=1,n] на плоскость [XY]. Полученный график называется допустимости предположения о линейной зависимости между перемен­ными. Если такое предположение допустимо, то необходимо выразить в количественном виде величину линейной связи. Для этого исполь­зуется выборочный коэффициент корреляции:

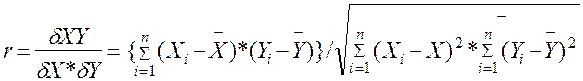
где n - количество измерений, Xi,Yi - i-е значения, X,Y - сред­ние значения, sx, sy - среднеквадратические отклонения перемен­ных X и Y соответственно.

В теории статистического анализа корреляционная связь опре­деляется как линейная зависимость в условиях нормальности расп­ределения анализируемых переменных. Поэтому для корректного при­менения корреляционных методов необходимо обосновать близость распределения переменных к нормальному и формы связи к линейной. В противном случае необходимо применять более сложные приемы анализа или другие коэффициенты связи.

Достаточно простой в вычислительном отношении способ про­верки нормальности эмпирического распределения состоит в оценке следующего отношения:

,

где C - среднее абсолютное отклонение, s - среднеквадратическое отклонение.

Если указанное неравенство выполняется, то можно говорить о нормальности эмпирических распределений и корректности примене­ния коэффициента корреляции как меры линейной статистической связи между переменными.

В общем случае на уровень преступности влияет множество фак­торных признаков. К ним относятся социально-экономические, геог­рафические и климатические, демографические и др., а также приз­наки, характеризующие силы и средства, степень организованности органа внутренних дел.

Однако даже при наличии сильной статистически значимой свя­зи между двумя переменными нельзя быть полностью уверенным в их причинно-следственной обусловленности, так как могут существо­вать другие причины (факторы), определяющие их совместную ста­тистическую взаимосвязь. Статистические выводы должны быть всег­да обоснованы надежной теоретической концепцией.

В то же время отсутствие статистически значимой связи не говорит об отсутствии причинно-следственных отношений, а заставляет искать другие пути и средства ее выявления, если содержа­тельная концепция и практический опыт указывают на ее возможное существование.

Дата добавления: 2014-01-20