Регрессионный анализ

Понятия корреляции и регрессии непосредственно связаны меж­ду собой. В корреляционном и регрессионном анализе много общих вычислительных приемов. Они используются для выявления причин­но-следственных соотношений между явлениями и процессами. Одна­ко, если корреляционный анализ позволяет оценить силу и направ­ление стохастической связи, то регрессионный анализ - еще и фор­му зависимости.

Регрессия может быть:

а) в зависимости от числа явлений (переменных):

- простой (регрессия между двумя переменными);

- множественной (регрессия между зависимой переменной (y) и несколькими объясняющими ее переменными (х1, х2...хn);

б) в зависимости от формы:

- линейной (отображается линейной функцией, а между изучае­мыми переменными существуют линейные соотношения);

- нелинейной (отображается нелинейной функцией, между изу­чаемыми переменными связь носит нелинейный характер);

в) по характеру связи между включенными в рассмотрение пе­ременными:

- положительной (увеличение значения объясняющей переменной приводит к увеличению значения зависимой переменной и наоборот);

- отрицательной (с увеличением значения объясняющей переменной значение объясняемой переменной уменьшается);

г) по типу:

- непосредственной (в этом случае причина оказывает прямое воздействие на следствие, т.е. зависимая и объясняющая перемен­ные связаны непосредственно друг с другом);

- косвенной (объясняющая переменная оказывает опосредован­ное действие через третью или ряд других переменных на зависимую переменную);

- ложной (нонсенс регрессия) - может возникнуть при поверх­ностном и формальном подходе к исследуемым процессам и явлениям. Примером бессмысленных является регрессия, устанавливающая связь между уменьшением количества потребляемого алкоголя в нашей стране и уменьшением продажи стирального порошка.

При проведении регрессионного анализа решаются следующие основные задачи:

1. Определение формы зависимости.

2. Определение функции регрессии. Для этого используют ма­тематическое уравнение того или иного типа, позволяющее, во-пер­вых, установить общую тенденцию изменения зависимой перемен­ной, а, во-вторых, вычислить влияние объясняющей переменной (или нескольких переменных) на зависимую переменную.

3. Оценка неизвестных значений зависимой переменной. Полу­ченная математическая зависимость (уравнение регрессии) позволя­ет определять значение зависимой переменной как в пределах ин­тервала заданных значений объясняющих переменных, так и за его пределами. В последнем случае регрессионный анализ выступает в качестве полезного инструмента при прогнозировании изменений со­циально-экономических процессов и явлений (при условии сохране­ния существующих тенденций и взаимосвязей). Обычно длина вре­менного отрезка, на который осуществляется прогнозирование, выбирается не более половины интервала времени, на котором прове­дены наблюдения исходных показателей. Можно осуществить как пас­сивный прогноз, решая задачу экстраполяции, так и активный, ведя рассуждения по известной схеме "если..., то" и подставляя раз­личные значения в одну или несколько объясняющих переменных рег­рессии.

Для построения регрессии используется специальный метод, получивший название метода наименьших квадратов. Этот метод име­ет преимущества перед другими методами сглаживания: сравнительно простое математическое определение искомых параметров и хорошее теоретическое обоснование с вероятностной точки зрения.

При выборе модели регрессии одним из существенных требова­ний к ней является обеспечение наибольшей возможной простоты, позволяющей получить решение с достаточной точностью. Поэтому для установления статистических связей вначале, как правило, рассматривают модель из класса линейных функций (как наиболее простейшего из всех возможных классов функций):

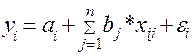
где bi, b2...bj - коэффициенты, определяющие влияние независимых переменных хij на величину yi; аi - свободный член; ei - слу­чайное отклонение, которое отражает влияние неучтенных факторов на зависимую переменную; n - число независимых переменных; N ­число наблюдений, причем должно соблюдаться условие (N. n+1).

Линейная модель может описывать весьма широкий класс различных задач. Однако на практике, в частности в социально-эконо­мических системах, подчас затруднительно применение линейных мо­делей из-за больших ошибок аппроксимации. Поэтому нередко ис­пользуются функции нелинейной множественной регрессии, допускающие линеаризацию. К их числу, например, относится производст­венная функция (степенная функция Кобба-Дугласа), нашедшая при­менение в различных социально-экономических исследованиях. Она имеет вид:

,

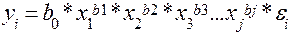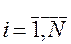
где b₀ - нормировочный множитель, b₁...b_j - неизвестные коэффи­циенты, e_i - случайное отклонение.

Используя натуральные логарифмы, можно преобразовать это уравнение в линейную форму:

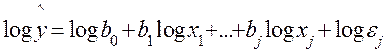
Полученная модель позволяет использовать стандартные проце­дуры линейной регрессии, описанные выше. Построив модели двух видов (аддитивные и мультипликативные), можно выбрать наилучшие и провести дальнейшие исследования с меньшими ошибками аппрокси­мации.

Существует хорошо развитая система подбора аппроксимирующих функций - методика группового учета аргументов (МГУА).

О правильности подобранной модели можно судить по результа­там исследования остатков, являющихся разностями между наблю­даемыми величинами y_i и соответствующими прогнозируемыми с по­мощью регрессионного уравнения величинами y_i. В этом случае для проверки адекватности модели рассчитывается средняя ошибка ап­проксимации:

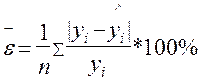
Модель считается адекватной, если e находится в пределах не более 15%.

Особо подчеркнем, что применительно к социально-экономичес­ким системам далеко не всегда выполняются основные условия адек­ватности классической регрессионной модели.

Не останавливаясь на всех причинах возникающей неадекват­ности, назовем лишь мультиколлинеарность - самую сложную пробле­му эффективного применения процедур регрессионного анализа при изучении статистических зависимостей. Под мультиколлинеарностью понимается наличие линейной связи между объясняющими переменны­ми.

Это явление:

а) искажает смысл коэффициентов регрессии при их содержа­тельной интерпретации;

б) снижает точность оценивания (возрастает дисперсия оце­нок);

в) усиливает чувствительность оценок коэффициентов к выбо­рочным данным (увеличение объема выборки может сильно повлиять на значения оценок).

Существуют различные приемы снижения мультиколлинеарности. Наиболее доступный способ - устранение одной из двух переменных, если коэффициент корреляции между ними превышает значение, рав­ное по абсолютной величине 0,8. Какую из переменных оставить ре­шают, исходя из содержательных соображений. Затем вновь прово­дится расчет коэффициентов регрессии.

Использование алгоритма пошаговой регрессии позволяет пос­ледовательно включать в модель по одной независимой переменной и анализировать значимость коэффициентов регрессии и мультиколли­неарность переменных. Окончательно в исследуемой зависимости ос­таются только те переменные, которые обеспечивают необходимую значимость коэффициентов регрессии и минимальное влияние мульти­коллинеарности.

Дата добавления: 2014-01-20