Социально-правовых процессов. Анализ динамики и прогнозирования

Анализ динамики и прогнозирования

Методы экстраполяции, в частности методы анализа и прогно­зирования временных рядов, дают возможность ответить на вопрос: что вероятнее всего произойдет при условии сохранения существую­щих тенденций? При этом предполагается определенная инерцион­ность развития процесса, проявляющаяся в сохранении темпов и направленности изменения основных количественных показателей на протяжении сравнительно длительного промежутка времени.

Основная идея экстраполяции заключается в нахождении по известным значениям динамического ряда других значений, лежащих за его пределами. Прогноз разрабатывается с обязательным привлечени­ем качественной информации, подтверждающей объективное существо­вание основной тенденции и обоснованность переноса ее в будущее.

При разработке экстраполяционных прогнозов статистическими методами выделяются два этапа. Первый этап - это обоснование су­ществования тенденции развития явления во времени и выбор анали­тической формы ее описания; второй - анализ и обоснование целе­сообразности распространения тенденции в будущее и собственно само аналитическое прогнозирование значений динамического ряда на заданный период времени.

Ввиду того, что уровни динамического ряда формируются под воздействием множества факторов, а также состоят из нескольких компонент (долговременных, циклических, сезонных и случайных), детальный анализ его поведения представляет собой довольно слож­ную задачу. Есть и другие особенности прогнозирования динамичес­ких рядов:

• развитие процессов в сфере правопорядка происходит непре­рывно, однако характеризующие их уровни динамического ряда соот­ветствуют определенным дискретным моментам времени (месяц, квар­тал, год), что приводит в некоторых случаях к потере части важ­ной информации;
• динамические ряды представлены часто сравнительно неболь­шим числом элементов, что затрудняет формальное применение экс­траполяционных методов прогнозирования;
• динамические ряды часто бывают автокоррелированными, т.е. их элементы тесно взаимосвязаны между собой, что требует приме­нения специальных, довольно сложных методов анализа;
• при построении многофакторных моделей по данным рядов ди­намики в некоторых случаях имеется тесная связь между независи­мыми переменными (мультиколлинеарность), что также требует при­менения специальных процедур;
• при исследовании взаимосвязей между процессами, характе­ризующимися рядами динамики, часто возникает явление сдвига во времени влияния одного фактора на другой (временной лаг).

Указанные особенности динамических рядов обусловливают необходимость глубокого содержательного анализа структуры описыва­емого ими явления и применения для их исследования разнообразных статистических процедур.

Как отмечалось ранее, в основе однофакторных статистических методов прогнозирования лежит гипотеза о том, что исходный дина­мический ряд состоит из устойчивой детерминированной компоненты и случайной составляющей. При этом выделяются три вида детерми­нированных компонент:

1) устойчивая долговременная тенденция, описываемая чаще всего гладкими апериодическими функциями типа линейной или квад­ратичной, - Y1(t);

2) циклическая долговременная тенденция, связанная с перио­дическими качественными изменениями процессов и описываемая ко­лебательными функциями с периодом меньшим, чем время действия устойчивой долговременной тенденции, но большим, чем у различных сезонных колебаний, - Y2(t);

3 ) циклическая устойчивая тенденция, связанная с периоди­ческими колебаниями уровней ряда за счет влияния сезонных факто­ров, меняющихся в течение дней недели, месяцев, времен года, - Y3(t).

Таким образом, общую модель динамического ряда можно предс­тавить в следующем виде:

где g(t) - случайная составляющая.

Анализ общей модели динамического ряда является сложной за­дачей как в теоретическом, так и в методическом плане. При этом используются различные статистические процедуры.

Для анализа устойчивой долговременной тенденции Y1(t) целе­сообразно применение методов экспоненциального и адаптивного сглаживания, скользящих средних и укрупнения интервалов, конеч­ных разностей, для оценки параметров моделей различных модифика­ций - метода наименьших квадратов. Изучение циклических компо­нент Y2(t) и Y3(t) целесообразно с помощью хорошо развитого ма­тематического аппарата спектрального анализа.

Одним из основных аналитических методов выделения долговре­менных тенденций динамического ряда является метод наименьших заключается в том, что для выбранной функции сглаживания опреде­ляются параметры, при которых сумма квадратов отклонений расчет­ных значений уровней Y(t), вычисленных по искомой функции от их фактических значений Y(t), была бы минимальной, а именно:

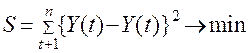
где n - число наблюдений ряда.

Выбор вида аналитической функции определяется теоретическим анализом сущности изучаемого явления и характером поведения ди­намического ряда в периоде основания прогноза: она может иметь вид прямой, параболы, гиперболы, экспоненты и т.д. или их раз­личных комбинаций.

При выборе вида функции в качестве тренда целесообразно учитывать следующие соображения. Линейный и экспоненциальный ти­пы трендов лучше использовать для прогнозирования инерционных временных рядов без насыщения, при этом надо учитывать, что экс­понента при больших временах носит взрывной характер. Степенные и логарифмические тренды лучше использовать, когда скорость из­менения значений ряда ниже экспоненциальной и характер процессов достаточно плавный, хотя эти тренды также не обладают свойством насыщения. Тренды гиперболического и S-образного типа предназна­чены для рядов с насыщением, характеризующихся небольшой скоро­стью изменения уровней.

Допустим, что аналитическая форма функции тренда выражается уравнением прямой линии Y(t) = a + b*t. Коэффициенты a и b из условия минимизации суммы квадратов отклонений определяются сле­дующими соотношениями:

При выборе вида функций из нескольких возможных предпочте­ние следует отдать той, у которой ошибка S меньше.

Важное место в задачах прогнозирования временных рядов от­водится методу экспоненциального сглаживания, которое осущест­вляется с помощью экспоненциально-взвешенных скользящих средних. При этом имеется возможность учитывать с большим весом наблюде­ния, имеющие большую информационную ценность, в частности, можно задавать большие веса более поздним наблюдениям по сравнению с ранними наблюдениями. Такая возможность придает гибкость в опи­сании динамического ряда.

К простейшим эмпирическим методам относятся метод сглаживания уровней путем укрупнения интервалов и метод скользящих средних. Достоинство их является простота и наглядность. К недостаткам, в частности метода скользящих средних, следует отнести искажение вида тенденции для коротких рядов динамики, трудность обоснования выбора интервала сглаживания, потерю нескольких уровней ряда и др.

Метод укрупнения интервалов является одним из самых простых эмпирических способов. Суть его состоит в том, что в результате анализа ряда выбирается соответствующий укрупненный интервал, в пределах которого складываются показатели уровней имеющегося ря­да, в результате чего получается новый выравненный ряд.

К простейшим экстраполяционным методам относятся методы последовательно увеличиваются или уменьшаются. Для рядов с сильно колеблющимися уровнями вычисление средних теряет смысл.

Дата добавления: 2014-01-20