КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные формулы комбинаторики. Задачи, цель которых – определение числа способов осуществление того или иного действия, называются комбинаторными
|
|
|
|
Задачи, цель которых – определение числа способов осуществление того или иного действия, называются комбинаторными, а наука, изучающая способы решения таких задач называется комбинаторикой.
Выборки без повторений.
|
 Если одна от другой отличается либо составом
Если одна от другой отличается либо составом
элементов, либо порядком их расположения
 | |||
 |
Если одно от другого отличаются только порядком расположения элементов
Если одно от другого отличаются хотя бы одним элементом (только составом).
|
|
|
 Если одна от другой отличается либо составом
Если одна от другой отличается либо составом
элементов, либо порядком их расположения
| |||||
 |  |
|
|
Правило суммы: если объект хÎХ может быть выбран n способами, а объект yÎY может быть выбран m способами, то выбор объекта «либо х, либо у» может быть осуществлён n+m способами.
Правило произведения: если объект хÎХ может быть выбран n способами и после каждого из таких выборов объект yÎY может быть выбран m способами, то выбор объекта «х и у» (упорядоченной пары (х, у)) может быть осуществлён nm способами.
Задание 1. Вычислить, используя формулы комбинаторики для выборок без повторений:
| Вычислить | Формула | Расчёт |

|  , n ³ m , n ³ m
| n =7³ m =3

|

|  , n ³ m , n ³ m
| n =____ m =____

|

|  , n ³ m , n ³ m
| n =____ m =____
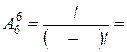
|

|  , n ³ m , n ³ m
| n =____ m =____

|
| Р 6 | Рm = m! | m =6 Р 6=6!=1·2·3·4·5·6=720 |
| Р 4 | Рm = m! | m =__ Р 4= |

| 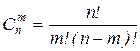 , n ³ m , n ³ m
| n =7³ m =3
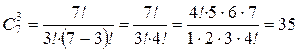
|
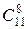
| 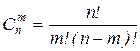 , n ³ m , n ³ m
| n =____ m =____

|
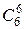
| 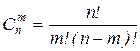 , n ³ m , n ³ m
| n =____ m =____

|

| 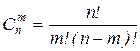 , n ³ m , n ³ m
| n =____ m =____
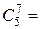
|
Задание 2. Вычислить, используя формулы комбинаторики для выборок с повторениями:
| Вычислить | Формула | Расчёт |
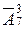
| 
| n =7; m =3

|

| 
| n =____ m =____

|
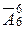
| 
| n =____ m =____

|
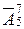
| 
| n =____ m =____

|

| 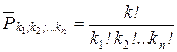 , k =S ki , k =S ki
| k 1=2; k 2=1; k 3=3; k =2+1+3=6

|
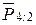
| 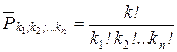 , k =S ki , k =S ki
| k 1=__; k 2=__; k =_______
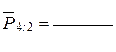
|

| 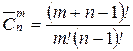
| n =7; m =3
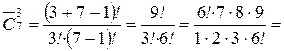
|

| 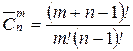
| n =____ m =____
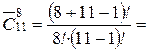
|

| 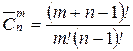
| n =____ m =____

|

| 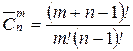
| n =____ m =____

|
Задача 1.
Сколько различных трёхзначных чисел можно составить, при условии, что цифры в числе не повторяются.
Решение:
Данная задача на размещения без повторений объёма m из данных n элементов (так как один вариант числа от другого может отличаться либо составом элементов____________, либо порядком их расположения ________________).
 , (n ³ m)
, (n ³ m)
n =_____________________________________ m =___________________________________

Заметим, что в данное число 720 вариантов вошли те «трёхзначные числа», которые таковыми не являются с точки зрения математики – это, например, числа________________________ («числа с нулём впереди»). Соответственно их нужно пересчитать и исключить из данной совокупности.
I способ расчёта: по классам
Разобьём все числа на десять классов (по виду первой цифры):
«1 класс» - числа с единицей впереди:………………………………………………………...;
«2 класс» - числа с двойкой впереди…………………………………………………………..;
«3 класс» - числа с тройкой впереди…………………………………………………………..;
«4 класс» - числа с четвёркой впереди: ……………………………………………………….;
«5 класс» - числа с пятёркой впереди: ………………………………………………………...;
«6 класс» - числа с шестёркой впереди: ………………………………………………………;
«7 класс» - числа с семёркой впереди: ………………………………………………………..;
«8 класс» - числа с восьмёркой впереди:..……………………………………………………;
«9 класс» - числа с девяткой впереди: ………………………………………………………...;
«10 класс» - числа с нулём впереди: ………………………………………………………….;
Соответственно, в каждом классе будет одинаковое число элементов:_________________
____________________________________________________________________________
II способ расчёта: комбинаторный
Ответ:__________.
Задача 2.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 491; Нарушение авторских прав?; Мы поможем в написании вашей работы!