Сколько различных десятизначных чисел можно составить, при условии, что цифры в числе не повторяются

Решение:

1. Данная задача очень похожа на предыдущую - на размещения без повторений:

, (n ³ m)

n =____________________________________; m =___________________________________

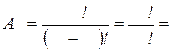
Заметим, что в данное число вариантов вошли те «десятизначные числа», которые таковыми не являются с точки зрения математики – это, например, числа________________________ («числа с нулём впереди»). Соответственно их нужно пересчитать и исключить из данной совокупности.

Разобьём все числа также на десять классов. Соответственно, в каждом классе будет одинаковое число элементов:___________________________________________________

____________________________________________________________________________

Ответ:__________.

2. Данная задача всё-таки относится к теме перестановки без повторений объёма m (так как один вариант числа от другого может отличаться только порядком расположения элементов________________________________________________).

,

m =__________________________________________________________________________

Далее аналогично, разобьём все числа также на десять классов. Соответственно, в каждом классе будет одинаковое число элементов:_________________________________

Ответ:__________.

Задача 3.

Сколько слов можно получить при перестановке букв слова «ОТЕЦ».

Решение:

Данная задача относится к теме перестановки без повторений объёма m:

____________________________________________________________________________

Ответ:__________.

Задача 4.

Сколько различных делегаций в составе трёх человек можно выбрать от коллектива, в котором десять человек.

Решение:

Данная задача на сочетания без повторений объёма m из данных n элементов (так как один вариант делегации от другого может отличаться только составом).

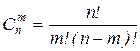, (n ³ m); n =________________________; m =_______________________;

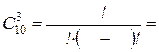
Ответ:__________.

Задача 5.

Сколько различных трёхзначных номеров можно составить, при условии, что цифры в числе могут повторяться.

Решение:

Данная задача на размещения с повторениями объёма m из повторяющихся элементов n различных классов.

_____________________________________________________________________

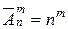Ответ:__________.

Задача 6.

Сколько слов можно получить при перестановке букв слова «ПАПА», «КОЛОКОЛ».

Решение:

Данная задача относится к теме перестановки с повторениями где элемент i -го класса (i =1,2,… n) повторяется k_i раз

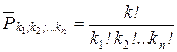, k =S k_i:

ü «ПАПА»

k =

k ₁=____(П); k ₂=____(А);

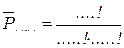
ü «КОЛОКОЛ»

k =

k ₁=____(К); k ₂=____(О); k ₃=____(Л);

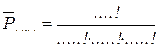
Ответ:__________.

Задача 7.

Дата добавления: 2014-01-20