Лекция № 1

Тема: Введение в курс медицинской и биологической физики. Биомеханика. Процессы переноса в биологических системах (часть 1)

План лекции:

1. Внутреннее трение (вязкость). Уравнение Ньютона

2. Ламинарное и турбулентное течение. Число Рейнольдса. Формула Пуазейля. Уравнение Бернулли

3. Методы определения вязкости крови

Биомеханикой называется раздел биофизики, в котором рассматриваются механические свойства живых тканей и органов, а также механические явления, происходящие как с целым организмом, так и с отдельными его органами.

Область биомеханики, в которой исследуется движение крови по сосудистой системе, называют гемодинамикой. Физической основой гемодинамики является гидродинамика.

Поэтому прежде чем приступить к изучению проблем, прямо относящихся к гемодинамике, необходимо рассмотреть основные положения гидродинамики. При этом необходимо помнить следующее:

а) при изучении жидкостей в покое нет необходимости различать реальные и идеальные жидкости. Их свойства однотипны;

б) при изучении движущихся жидкостей необходимо дополнительно учитывать силы трения, возникающие в реальных жидкостях, т.е. их вязкость.

К реальным жидкостям относят все жидкости, встречающиеся в природе.

Для реальных жидкостей характерно возникающие в них при движении касательных напряжений, или трения, которое носит название вязкости.

Идеальные жидкости – это модель. Идеальные жидкости характеризуются абсолютной неизменяемостью объема и полным отсутствием вязкости, т.е. сил трения при их движения.

1. При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называют внутренним трением или вязкостью. Рассмотрим течение вязкой жидкости между двумя твердыми пластинками (рис. 1), из которых нижняя неподвижна, а верхняя движется со скоростью v_b. Условно представим жидкость в виденескольких слоев 1, 2, 3 и т. д. Слой, «прилипший» ко дну, неподвижен. По мере удаления от дна (нижняя пластинка) слои жидкости имеют все большие скорости (v1 < v2 > v3 <…), максимальная скорость v_B будет у слоя, который «прилип» к верхней пластинке. Слои воздействуют друг на друга. Так, например, третий слой стремится ускорить движение второго, но сам испытывает торможение с его стороны, а ускоряется четвертым слоем и т. д.

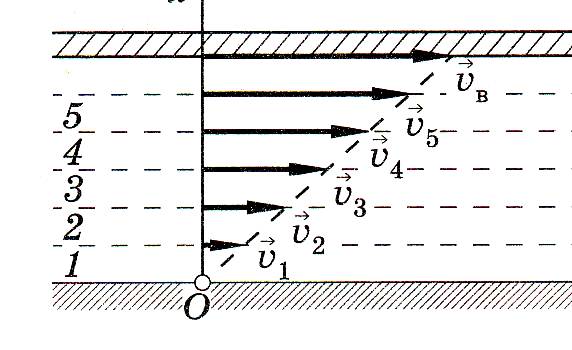
Рис.1

Сила внутреннего трения пропорциональна площади S взаимодействующих слоев и тем больше, чем больше их относительная скорость. Так как разделение на слои условно, то принято выражать силу в зависимости от изменения скорости на некотором участке в направлении x, перпендикулярном скорости, отнесенного к длине этого участка, т. е. от величины 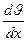- градиента скорости (скорости сдвига):

Fтр = η 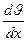S (1)

Это уравнение Ньютона. Здесь η — коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью(или просто вязкостью ). Вязкость зависит от состояния и молекулярных свойств жидкости (или газа).

Единицей вязкости является паскаль-секунда (Па • с). В системе СГС вязкость выражают в пуазах (П): 1 Па • с = 10 П.

Для многих жидкостей вязкость не зависит от градиента скорости (вязкость постоянна), такие жидкости подчиняются уравнению Ньютона (1), их называют ньютоновскими. Это обычные среды: воздух, вода, глицерин, ртуть и т.д.Жидкости, не подчиняющие уравнению (1), имеющие не постоянную вязкость, относят к неньютоновским. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновских — аномальной.

Жидкости, состоящие из сложных и крупных молекул, например растворы полимеров, и образующие благодаря сцеплению мо­лекул или частиц пространственные структуры, являются неньютоновскими. Их вязкость при прочих равных условиях много больше, чем у простых жидкостей. Увеличение вязкости происхо­дит потому, что при течении этих жидкостей работа внешней си­лы затрачивается не только на преодоление истинной, ньютонов­ской, вязкости, но и на разрушение структуры. Кровь является неньютоновской жидкостью, т.к. представляет собой суспензию форменных элементов в плазме. Форменные элементы, на которые в норме приходится 45% объема крови, включают эритроциты, лейкоциты и тромбоциты. Эритроциты намного многочисленнее других форменных элементов и поэтому полностью определяют механические свойства крови.

Плазма крови – раствор крупных молекул, но при масштабах движения и при скоростях сдвига, обычно встречающихся в кровеносных сосудах, ее можно считать однородной ньютоновской жидкостью с вязкостью 0.0012 – 0.0016 Па.с (37град С).

В мельчайших кровеносных сосудах кровь нельзя полагать однородной жидкостью, т.к. диаметры эритроцита (8 мкм) и капилляра сравнимы по величине. В сосудах же диаметром более 100 мкм кровь может рассматриваться как однородная среда, поскольку характерные размеры микроструктуры много меньше характерных размеров течения. Поэтому в крупных сосудах кровь можно считать ньютоновской жидкостью с вязкостью 0.004 Па.с (4 мПа.с или 40 мП) при 37 градС.

В определенном диапазоне скоростей сдвига кровь является неньютоновской жидкостью. При скорости сдвига выше 100 1/с вязкость не зависит от скорости сдвига (ньютоновская жидкость). Доказано, что физической основой зависимости кажущейся вязкости крови от скорости сдвига, определяющей ее свойства как неньютоновской жидкости, могут служить изменения суспензионной стабильности крови и связанная с этим агрегация эритроцитов. Предполагают, что свойства крови как неньютоновской жидкости зависят также от способности эритроцитов к деформации. При низких скоростях сдвига (ниже 100 1/с) в крови имеются агрегаты эритроцитов в виде монетных столбиков. Эти агрегаты распадаются по мере увеличения скорости сдвига, вязкость снижается (крупные сосуды). Благодаря дисковидной форме клеток и эластичности оболочки суспензия эритроцитов обладает сравнительно невысокой вязкостью, что важно для уменьшения нагрузки на сердце, которое прокачивает кровь по кровеносным сосудам. Увеличение жесткости стенок эритроцитов при патологических процессах приводит к возрастанию вязкости крови и к ухудшению кровообращения.

2. Течение вязкой жидкости по трубам представляет для медици­ны особый интерес, так как кровеносная система состоит в основ­ном из цилиндрических сосудов разного диаметра.

Вследствие симметрии ясно, что в трубе частицы текущей жидкости, равноудаленные от оси, имеют одинаковую скорость. Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; примыкающий к трубе слой жидкости неподвижен.

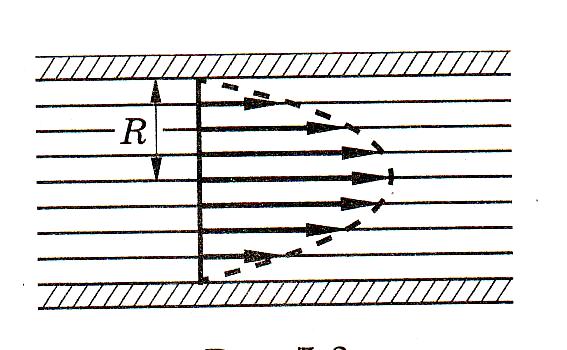
Рис.2

Установим, от каких факторов зависит объем Q жидкости, протекающий через горизонтальную трубу за 1 с, или объемная скорость кровотока, или объемный расход крови:

Q = (2)

Эта зависимость носит название формулы Пуазейля, где η — вязкость жидкости, p1- p2 — разность давле­ний, поддерживаемая на торцах трубы длиной l. Как видно из (2), при заданных внешних условиях (p₁ и p2) через трубу протекает тем больший объем жидкости, чем меньше ее вязкость и больше радиус трубы.

Проведем аналогию между формулой Пуазейля (2) и законом Ома для участка цепи без источника тока. Разность потенциалов соответствует разности давлений на концах трубы, сила тока — объему жидкости, протекающей через сечение трубы в 1 с, электрическое сопротивление — гидравлическому сопротивлению:

Х = 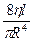(3)

Гидравлическое сопротивление тем больше, чем больше вязкость η, длина l трубы и меньше площадь поперечного сечения. Аналогия между электрическим и гидравлическим сопротивлениями позво­ляет в некоторых случаях использовать правило нахождения электрического сопротивления последовательного и параллельного соеди­нений проводников для определения гидравлического сопротивления системы последовательно или параллельно соединенных труб (Рис. 3)

Рис. 3

Закон Ома	Формула Пуазейля
I = U/R	Q = π R^4/8 η · (p1- p2)/ l или Q = (p1- p2)/ Х
U	p1- p2
I	Q
R	Х = 8 η 1/(π R^4)

Для труб с переменным сечением заменим (Р1- Р2)/ l на градиент давления dp/dl и тогда:

Q = 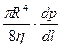(4)

Т.к. Q = const (жидкость несжимаема), то градиент давления больше в трубах меньшего радиуса. Если труба сужается, то скорость движения увеличивается. Но если труба не жесткая (сосуды), то объемный расход будет одинаков во всех точках только при стационарном потоке.

Существует два характера течения жидкости: ламинарное (слоистое, установившееся, стационарное) и турбулентное (вихревое, неустановившееся, нестационарное). Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы и определяется числом Рейнольдса:

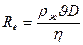, (5)

где 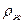- плотность жидкости, D – диаметр трубы.

Если число Рейнольдса больше некоторого критического (Re>Re кр), то движение жидкости турбулентное. Если число Рейнольдса меньше критического (Re<Re кр), то течение ламинарное.

Объясняя физический смысл числа Рейнольдса, следует обратить внимание на следующее:

а) когда Re<<1, мы можем сказать, что вязкие силы преобладают, а инерционные пренебрежимо малы. Например, на уровне микрососудов (сосуды диаметром порядка 100 мкм и менее) типичные числа Рейнольдса меньше единицы и течение можно рассматривать как чисто вязкое;

б) когда Re>>1, напротив, преобладают инерционные силы, а вязкость (во всех областях, кроме пограничных) лишь незначительно изменяет характер течения. Например, для крови в крупных артериях, в венах.

Так как число Рейнольдса зависит от вязкости и плотности жидкости, то удобно ввести их отношение, называемое кинематическойвязкостью :

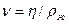
Кинематическая вязкость полнее, чем динамическая, учитывает влияние внутреннего трения на характер течения жидкости или газа. Так, вязкость воды приблизительно в 100 раз больше чем воздуха (при 0 °С), но кинематическая вязкость воды в 10 раз меньше, чем воздуха, и поэтому вязкость сильнее влияет на ха­рактер течения воздуха, чем воды.

Как видно из (5), характер течения жидкости или газа суще­ственно зависит от размеров трубы. В широких трубах даже при сравнительно небольших скоростях может возникнуть турбулент­ное движение. Так, например, в трубке диаметром 2 мм течение ве­ды становится турбулентным при скорости более 127 см/с, а в трубе диаметром 2 см — уже при скорости примерно 12 см/с (температура16 °С). Течение крови по такой трубе стало бы турбулентным при скорости 50 см/с, но практически в кровеносных сосудах диаметром 2 см турбулентное течение возникает даже при меньшей скорости.

Течение крови в артериях в норме является ламинарным, не­большая турбулентность возникает вблизи клапанов сердца. При патологии, когда вязкость бывает меньше нормы, число Рей­нольдса может превышать критическое значение и движение станет турбулентным.

Турбулентное течение связано с дополнительной затратой энергии при движении жидкости, что в случае крови приводит к добавочной работе сердца. Шум, возникающий при турбулентном течении крови, может быть использован для диагностирования заболеваний. Этот шум прослушивают на плечевой артерии при измерении давления крови.

Течение воздуха в носовой полости в норме ламинарное. Одна­ко при воспалении или каких-либо других отклонениях от нормы оно может стать турбулентным, что повлечет дополнительную ра­боту дыхательных мышц.

Число Рейнольдса является критерием подобия. При модели­ровании гидро- и аэродинамических систем, в частности крове­носной системы, модель должна иметь такое же число Рейнольд­са, как и натура, в противном случае не будет соответствия между ними.

Средние числа Рейнольдса

Аорта 1200 – 5800 Капилляры 0.001 – 0.003

Большие Венулы,

артерии 1000 – 100 малые вены 0.01 – 1

Малые Большие вены 100 – 600

артерии,

артериолы 10 – 0.01 Полые вены 600 – 1000

Для установившихся течений, очевидно, что через любое поперечное сечение трубы в единицу времени должна протекать одна и та же масса жидкости, то есть:

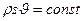(это уравнение неразрывности струи).

Для несжимаемых жидкостей: 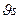=const или Q = const, т.к. Q = 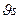, то есть скорость движения жидкой струи обратно пропорциональна ее поперечному сечению.

Как известно, в покоящейся жидкости действуют два рода сил: силы тяжести и разности давлений. Эти же силы действуют и в движущейся реальной жидкости, но к ним присоединяются еще и силы трения.

В 1738 г. Д.Бернулли вывел чрезвычайно важное соотношение для установившегося движения струи идеальной несжимаемой жидкости, получившее название уравнения Бернулли:

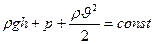, (7)

где - гидростатическое давление (или удельная потенциальная энергия сил тяжести жидкости);

p - статическое давление (или удельная потенциальная энергия сил давления);

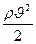- динамическое давление (или удельная кинетическая энергия).

Сумма трех давлений составляет полное давление движущейся жидкости. Уравнение Бернулли выражает собой закон сохранения энергии движущейся жидкости. Это означает, что для идеальной и несжимаемой текущей жидкости отдельные виды механической энергии могут изменяться, но при этом сумма их остается неизменной.

При применении уравнения Бернулли к реальным жидкостям необходимо учитывать силы трения, возникающие при их движении.

3. Совокупность методов измерения вязкости называют вискозиметрией, а приборы, используемые для таких целей, — вискозиметрами.Рассмотрим наиболее распространенные методы вискозиметрии.

Капиллярный метод основан на формуле Пуазейля и заключаетсяв измерении времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений. В одних конструкциях градиент давления создается массой столба исследуемой жидкости (вискозиметр Оствальда). В других – градиент давления обеспечивается каким-либо источником (вискозиметр Гесса).

Капиллярный вискозиметр применяется для определения вязкости крови (Рис.4).

Рис.4

Капиллярными вискозиметрами измеряют вязкость от значений 10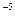Па • с, свойственных газам, до значений 10⁴ Па • с, характерных для консистентных смазок.

Метод падающего шарика используется в вискозиметрах, основанных на законе Стокса. Измеряя скорость равномерного падения шарика, можно найти вязкость данной жидкости.

Предел измерений вискозиметров с движущимся шариком со­ставляет 6 • 10⁴ - 250 Па • с.

Применяются также ротационные вискозиметры, в которых жидкость находится в зазоре между двумя соосными телами, на­пример цилиндрами. Один из цилиндров (ротор) вращается, другой неподвижен. Вязкость измеряется по угловой скорости ро­тора, создающего определенный момент силы на неподвижном цилиндре, или по моменту силы, действующему на неподвижный цилиндр, при заданной угловой скорости вращения ротора.

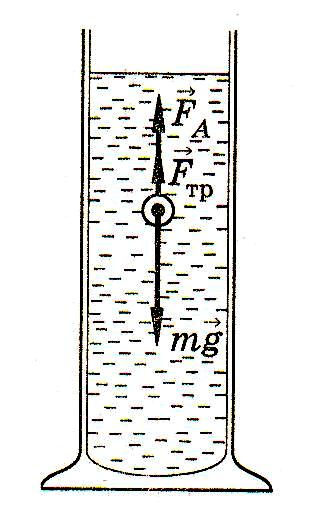
Рис.5

С помощью ротационных вискозиметров определяют вязкость жидкостей в интервале 1 —10⁵ Па • с, т. е. смазочных масел, рас­плавленных силикатов и металлов, высоковязких лаков и клеев, глинистых растворов и т. п.

В ротационных вискозиметрах можно менять градиент скорости задавая разные угловые скорости вращения ротора. Это позволяет измерять вязкость при разных градиентах.

В настоящее время в клинике для определения вязкости крови используют вискозиметр Гесса с двумя капиллярами (Рис.5). Два одинаковых капилляра 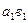и 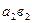соединены с двумя трубочками 1 и 2. Посредством резиновой груши или втягивая воздух ртом через наконечник 3, поочередно благодаря тройнику с краном 4,заполняют капилляр 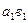и трубоч­ку 1до отметки 0 дистиллированной водой, а капилляр 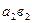и тру­бочку 2до отметки 0 — исследуемой кровью. После этого теми же способами одновременно перемещают обе жидкости до тех пор, по­ка кровь не достигнет цифры 1, а вода — другой отметки в своей трубке. Так как условия протекания воды и крови одинаковы, то объемы наполнения трубок 1и 2будут различными вследствие то­го, что вязкости этих жидкостей неодинаковы. Хотя кровь и явля­ется неньютоновской жидкостью, используем с некоторым прибли­жением формулу Пуазейля и запишем очевидную пропорцию:

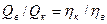(8)

Рис.5

Учитывая, что общий объем Vжидкости при равномерном ее течении связан с Q формулой V = Q t, где t— время истечения жидкости, вместо (8) получаем:

,

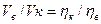где Vк — объем крови в трубке 2от отметки 0 до отметки 1; Vв - объем воды в трубке 1от отметки 0 до отметки, полученной при измерении; η_к и η_в — соответственно вязкость крови и воды. Отношение вязкости крови к вязкости воды при той же температуре называют относительной вязкостью крови.

В вискозиметре Гесса объем крови всегда одинаков, а объем воды отсчитывают по делениям на трубке 1, поэтому непосредственно получают значение относительной вязкости крови. Для удобства отсчета сечения трубок 1и 2делают различными так, что, несмотря на разные объемы крови и воды, их уровни в трубках будут примерно одинаковы.

Вязкость крови человека в норме 4—5 мПа • с, при патологии колеблется от 1,7 до 22,9 мПа • с, что сказывается на скорости оседания эритроцитов (СОЭ). Венозная кровь обладает несколько большей вязкостью, чем артериальная. При тяжелой физической работе увеличивается вязкость крови. Некоторые инфекционные заболевания увеличивают вязкость крови, другие же, например брюшной тиф и туберкулез, — уменьшают.

Дата добавления: 2014-01-20