Задачи безусловной оптимизации

Тема 1. Введение (продолжение)

Лекция №2

План на летне-оздоровительный сезон

Основой для составления служит диагностическая карта, составленная по результатам медико-педагогического исследования детей. Здесь важно на основе диагностических данных и условий предусмотреть использование в полной мере психо-гигиенических и эколого-природных факторов спрограммировать целостный режим.

Таким образом, от правильного планирования зависит система подачи знаний, выработка умений развитие и воспитание детей; назначение планирования состоит в том, чтобы обеспечить высокие конечные результаты.

Постановка и схема решения задачи

Как отмечалось ранее, задачи безусловной оптимизации имеют вид:

.

Такая постановка математической задачи подразумевает, что из содержания экономической задачи не вытекает никаких ограничений на допустимое множество, т.е. что .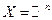

Замечание. Понятно, что не всякая функция определена на всем пространстве 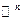, т.е. возможны случаи, что 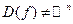. Однако в таких случаях ограничения (физические или экономические) на естественную область определения должны вытекать из ограничений реальной экономической задачи. В противном случае построенная математическая модель будет неадекватной исследуемой экономической задаче.

Далее будем предполагать, что функция 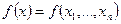дважды непрерывно дифференцируема всюду на области определения .

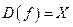Схема решения задачи может выглядеть следующим образом:

1⁰. Выясняется, имеет ли 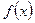глобальный максимум (минимум) на 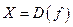. Если бы множество 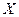было непусто, ограничено и замкнуто, то можно было бы воспользоваться теоремой Вейерштрасса. Таким образом, теоремой Вейерштрасса непосредственно воспользоваться не удается. В этом случае может помочь оценка характера поведения функции при стремлении ее аргументов к бесконечности. Так, например, если при 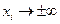значение функции стремится к 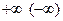, то глобального максимума (минимума) заведомо не существует.

Если же удается выделить ограниченное замкнутое множество 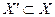, в некоторой точке 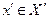которой значение функции больше (соответственно, меньше), чем в любой точке из оставшейся части 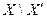множества 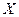, то она имеет глобальный максимум (соответственно, минимум) на множестве 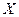, причем он будет расположен в множестве 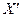(рис. 1). Этот вывод непосредственно вытекает из теоремы Вейерштрасса.

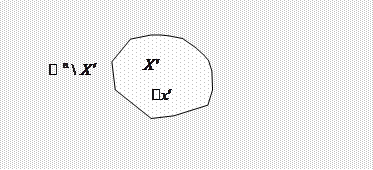Рис. 1. Множество 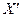замкнуто;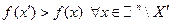

Если выясняется, что глобального максимума (минимума) нет, то задача не имеет решения, и нужно пересмотреть ее постановку. Если выясняется, что глобальный максимум (минимум) существует, следует перейти к его отысканию.

2⁰. Находятся все точки локального максимума (минимума).

3⁰. Вычисляются значения функции 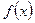во всех найденных точках локального максимума (минимума) и выбираются точки с наибольшим (наименьшим) значением функции. Они и составят решение задачи.

Замечание. На самом деле для нахождения точек глобального максимума (минимума) достаточно найти все стационарные точки (т.е. точки, в которых ) и выбрать те из них, в которых значение функции максимально. При этом не обязательно устанавливать наличие и вид экстремума в стационарных точках. Дело, правда, осложняется, если стационарных точек окажется бесконечное множество.

Дата добавления: 2014-01-20