Теорема. Детерминантный критерий знакоопределенности квадратичной формы с линейными условиями связи на переменные

Детерминантный критерий знакоопределенности квадратичной формы с линейными условиями связи на переменные

Квадратичная форма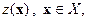

1) положительна тогда и только тогда, когда ;

2) отрицательна тогда и только тогда, когда ;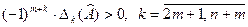

3) неотрицательна тогда и только тогда, когда

;

4) неположительна тогда и только тогда, когда

;

5) знакопеременна – в остальных случаях.

Замечание 1. Заметим, что критерии знакоопределенности квадратичной формы с линейными ограничениями отличаются от аналогичных критериев Сильвестра для квадратичных форм без ограничений следующими моментами:

а) составляется не обычная матрица квадратичной формы, а окаймленная;

б) проверка начинается не с миноров первого порядка, а с миноров порядка ;

в) знак каждого исследуемого минора отличается от аналогичного в критерии Сильвестра постоянным множителем .

Для большего удобства при использовании и для лучшего запоминания можно несколько иначе сформулировать эти правила. А именно:

1) составляется окаймленная матрица квадратичной формы;

2) определяется знак выражения и все исследуемые миноры рассматриваются с этим знаком;

3) вычисляется значение и исследование начинается с миноров этого порядка (причем все рассматриваемые миноры включают матрицу минора );

4) при сделанных в п.п.1–3 оговорках процедура исследования совпадает с таковой для квадратичных форм без ограничений:

- если знаки всех миноров положительны, то квадратичная форма положительна; если некоторые из знаков заменяются нулями – квазиположительна (в обоих случаях – неотрицательна);

- если знаки миноров чередуются, начиная с минуса, то квадратичная форма отрицательна; если некоторые из знаков заменяются нулями – квазиотрицательна (в обоих случаях – неположительна);

- если ни первое, ни второе правила знаков не соблюдаются, то квадратичная форма знакопеременна.

Таким образом, в случае n = 2, m = 1 нужно рассмотреть всего один минор: 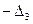; в случае n = 3, m = 1 – миноры третьего и четвертого порядка со знаком минус; в случае n = 3, m = 2 – один минор пятого порядка со знаком плюс и т.д.

Замечание 2. Условие 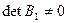не является существенным ограничением метода, так как

а) если 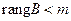, то из системы можно исключить линейно зависимые строки и придти к матрице полного ранга меньшего размера;

б) если же 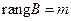, но , то перенумерацией переменных можно добиться того, чтобы выполнялось условие .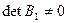

Дата добавления: 2014-01-20