Оценка чувствительности экстремального значения целевой функции к изменению констант в условиях связи

Схема отыскания условного локального экстремума методом Лагранжа

1. Проверяется выполнение условия Якоби: .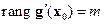

Если для каких-то точек условие Якоби не выполняется, то эти точки исследуются особо.

Если условие Якоби не выполняется ни в одной точке допустимого множества, то следует попытаться упростить условия связи, в том числе исключить связи, градиенты функций которых линейно зависят от остальных. При этом, однако, нужно удостовериться, что допустимое множество не изменилось.

2. Составляется функция Лагранжа: .

3. Выписываются необходимые условия первого порядка: и решается соответствующая система. Тем самым находятся точки, подозрительные на условный экстремум, и значения множителей Лагранжа для каждой точки.

4. Выписывается окаймленная матрица Гессе в общем виде (без подстановки координат найденных точек) и вычисляется ее значение для каждой стационарной точки.

При этом необходимо следить, чтобы левая квадратная часть окаймляющей матрицы Якоби 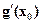была невырожденной. В противном случае следует перенумеровать переменные таким образом, чтобы это условие соблюдалось.

5. Для каждой точки вычисляются значения (или только знаки) выражений вида 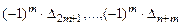(модифицированных угловых миноров) – см. табл.1.

а) Если все они положительны, то в данной точке имеет место условный минимум.

б) Если знаки чередуются, начиная с минуса, то в данной точке максимум.

в) Если оба указанных правила (а и б) «грубо нарушаются», т.е. в некоторой позиции вместо «+» имеем «–» или наоборот, то в данной точке экстремума нет.

г) Если одно из указанных правил (а или б) «мягко нарушается», т.е. некоторые знаки заменяются нулями, то необходимо исследовать все главные миноры (умноженные на ) порядка и выше, содержащие угловой минор . При этом возможны два случая:

г1) Правило знаков для главных миноров «грубо нарушается», т.е. хотя бы один из миноров имеет знак, противоположный требуемому знаку углового минора данного порядка. В этом случае экстремума в данной точке нет.

г2) Правило знаков для главных миноров «мягко нарушается», т.е. миноры либо имеют те же знаки, что и угловые миноры такого же порядка, либо равны нулю. В этом случае о наличии или отсутствии экстремума в данной точке ничего сказать нельзя – нужны дополнительные исследования.

6. Вычисляются значения целевой функции для каждой найденной точки экстремума.

Таблица 1. Угловые миноры, исследуемые при определении знакоопределенности окаймленной матрицы Гессе при различных значениях n и m

		–	–
			–

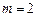
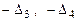
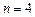
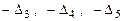
Приведенная схема в части уточнения наличия и квалификации условного экстремума аналогична схеме для безусловного экстремума с той лишь разницей, что исследованию подлежат лишь миноры порядка 2т+1 и более (включающие угловой минор), умноженные на , где т – число ограничений.

Замечание. Угловые миноры окаймленной матрицы Гессе всегда равны нулю, а минор всегда неположителен.

Пример

Методом Лагранжа найти точки условного экстремума и экстремальные значения функции при условии .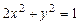

Решение

1. Проверим выполнение условия Якоби: , что невозможно, так как в этой точке не выполняется условие 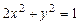. Значит, методом Лагранжа можно пользоваться без ограничений.

.

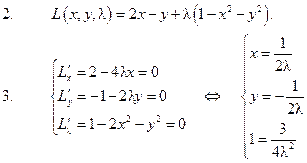
5. .

Здесь удобно находить значение углового минора в общем виде (без подстановки в матрицу координат найденных стационарных точек). Это сэкономит время и сокращает объем вычислений. При последнем упрощении использован тот факт, что искомые точки связаны условием .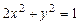

6. Вычисляем экстремальные значения целевой функции.

Ответ: - точка максимума, ; - точка минимума, .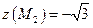

Посмотрим, являются ли найденные экстремумы глобальными. В данном случае допустимое множество не пусто, ограничено и замкнуто, а целевая функция непрерывна на . Значит, по теореме Вейерштрасса, целевая функция имеет на допустимом множестве глобальный максимум и глобальный минимум. Но так как глобальный максимум является также и локальным максимумом, а в данной задаче локальный максимум единственный, то он и будет тем самым глобальным максимумом. То же можно сказать и про минимум.

Замечание. При исследовании функции на условный экстремум с помощью окаймленной матрицы Гессе требовалось соблюдение условия , где 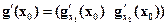. Несоблюдение этого условия может привести к невозможности сделать окончательный вывод о наличии или отсутствии экстремума. Если все же указанное условие не выполняется, а , то достаточно поменять местами переменные (записать их в другом порядке), чтобы это условие соблюдалось. Покажем это на примере.

Метод Лагранжа позволяет не только находить точки условного экстремума, но также и оценивать чувствительность экстремального значения целевой функции к изменению констант в условиях связи . А именно, множитель Лагранжа показывает, на сколько единиц изменится экстремальное значение целевой функции при увеличении константы на единицу (если эта единица достаточно мала).

Проиллюстрируем данное свойство для случая двух переменных и одного условия связи (рис. 8).

Итак, пусть имеем задачу

и некоторое ее решение . Обозначим .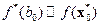

Изменим «слегка» константу в условии связи, т.е. вместо возьмем и решим новую задачу

.

Предположим, что она имеет решение, «близкое» к , обозначим его , а значение целевой функции .

Рис. 8. Иллюстрация зависимости оптимальной точки и оптимального значения целевой функции от константы в условии связи ()

При определенных ограничениях (окаймленная матрица Гессе в точке локального максимума или минимума отрицательно или положительно определена) решение задачи

,

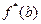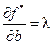непрерывно зависящее от , а значение целевой функции также непрерывно зависит от , причем функция дифференцируема по и , где 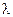– множитель Лагранжа, значение которого получается при решении задачи. Заметим, что 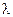тоже непрерывно зависит от .

Если приращение константы , т.е. , достаточно мало, то , и тогда

.

Таким образом, не решая заново задачу, мы можем оценить, насколько изменится оптимальное значение целевой функции, если изменить константу в условии связи на небольшую величину.

Аналогичный вывод справедлив и в общем случае переменных и условий связи

.

Если даем приращение одной константе в условии связи, то имеем приближенное равенство

,

а в общем случае, так как , получим .

Таким образом, если условия связи описывают ресурсные ограничения, а целевая функция – прибыль или доход, мы можем судить, объемы (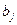) каких ресурсов целесообразно увеличить, если представляется такая возможность (например, за счет имеющихся денежных резервов или уменьшения других ), а объемы каких – не целесообразно. Так, есл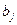и и 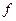измеряются в одних и тех же денежных единицах, то выгоднее увеличивать объем 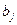того ресурса, для которого множитель Лагранжа больше. Если , то, по-видимому, нужно не увеличивать объем такого ресурса, а сокращать.

Если объемы ресурсов (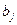) исчисляются в натуральном выражении, то сравнивать следует не значения , а их отношения к ценам ресурсов , т.е. .

Действительно,

,

где – дополнительные вложения денежных ресурсов (стоимость увеличения объема ресурса на ). Таким образом, дополнительное вложение одной денежной единицы в ресурс , используемый в производстве, принесет дополнительную прибыль(доход) в размере денежных единиц.

Если целевая функция описывает доход, то для вычисления приращения прибыли следует из дополнительного дохода, получаемого за счет увеличения объема ресурса, вычесть дополнительные расходы на его приобретение: .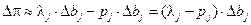

[1] В этом случае какой-то из угловых миноров обязательно будет равен нулю.

[2] – это матрица вторых производных функции Лагранжа только по переменным (без).

Дата добавления: 2014-01-20