Меры информации синтетического уровня

Меры информации прагматического уровня

Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цели. (А.А. Харкевич). Если до получения информации вероятность достижения цели равнялась p₀, а после ее получения — р₁, то ценность информации определяется как логарифм отношения р₁/р₀: I=log₂ р₁ - log₂ р₀ = log₂ (р₁/ р₀).

Таким образом, ценность информации при этом измеряется в единицах информации, в данном случае в битах.

Дальнейшее развитие данного подхода базируется на статистической теории информации и теории решений. Сущность метода состоит в том, что, кроме вероятностных характеристик неопределенности объекта, после получения информации вводятся функции штрафов или потерь и оценка информации производится в результате минимизации потерь.

Количественная оценка информации этого уровня не связана с содержательной стороной информации, а оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.

Для измерения информации на синтаксическом уровне вводятся два параметра:

1) объем информации (данных) — V (объемный подход) и

2) количество информации — I (энтропийный подход).

Объем информации V (объемный подход). Информация передается в виде сообщения, представляющего собой совокупность символов какого-либо алфавита. Если теперь количество информации, содержащейся в сообщении из одного символа, принять за единицу, то объем информации (данных) V в любом другом сообщении будет равен количеству символов (разрядов) в этом сообщении. Единица измерения информации (данных) соответственно будет меняться, например для разных алфавитов.

В десятичной СС единицей измерения информации будет дит (десятичный разряд). Cообщение в виде n-разрядного числа имеет объем данных V_д = n дит.(2003 => V_д = 4 дит).

В двоичной CC единицей измерения информации будет — бит (bit — binary digit — двоичный разряд). В этом случае сообщение в виде n-разрядного числа имеет объем данных V = n бит. (11001011 => V = 8 бит)

Укрупненная единица измерения «байт»=8 бит. Более крупные единицы измерения:

1 Кбайт = 1024 байт = 2¹⁰ байт;

1 Мбайт = 1024 Кбайт = 2²⁰ байт = 1 048 576 байт;

1 Гбайт = 1024 Мбайт = 2³⁰ байт = 1 073 741 824 байт;

1 Тбайт = 1024 Гбайт = 2⁴⁰ байт = 1 099 511 627 776 байт;

Далее Пета (P), Экса (E), Зета (Z), Йотта (Y).

Количество информации I (энтропийный или вероятностный подход). Факт получения информации всегда связан с уменьшением разнообразия или неопределенности (энтропии) системы. Количество информации в сообщении определяется как мера уменьшения неопределенности состояния данной системы после получения сообщения. Неопределенность может быть интерпретирована в смысле того, насколько мало известно наблюдателю о данной системе. Как только наблюдатель выявил что-нибудь в физической системе, энтропия системы снизилась, так как для наблюдателя система стала более упорядоченной.

Примеры использования вероятностного подхода:

1) Подбрасывание игральной кости, имеющей N граней. Результаты: выпадение каждой грани со знаками 1, 2…N Þ вероятность выпадения одной любой стороны равновероятны. энтропия по формуле Хартли: H=log₂N.

2) Вероятность выпадения различных букв в тексте для каждой буквы разные, т.е. не равновероятно.

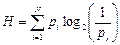
Формула Шеннона:

Если алфавит состоит из двух знаков: 0 или 1 Þ выпадение этих знаков равновероятно. Т.о. количество информации в двоичном слове = числу знаков в нем.

Таким образом, при энтропийном подходе под информацией понимается количественная величина исчезнувшей в ходе какого-либо процесса (испытания, измерения и т. д.) неопределенности. При этом в качестве меры неопределенности вводится энтропия Н, а количество информации равно:

I = Нарr - Haps, (1)

где Нарr — априорная энтропия о состоянии исследуемой системы или процесса.

Haps— апостериорная энтропия.

Апостериори (от лат. a posteriori — из последующего) — происходящее из опыта (испытания, измерения). Априори — (от лат. a priori — из предшествующего) — понятие, характеризующее знание, предшествующее опыту (испытанию), и независимое от него.

В случае когда в ходе испытания имевшаяся неопределенность снята (получен конкретный результат), т. е. H_aps = 0, количество полученной информации совпадает с первоначальной энтропией.

Н(А) = log_mN – мера была предложена американским ученым Р. Хартли в 1928 г. В зависимости от основания логарифма m применяют следующие единицы измерения:

1. Биты — при этом основание логарифма равно 2:
Н(А) = log₂N. (2.4)

2. Наты — при этом основание логарифма равно е:
H = lnN;

3. Диты — при этом основание логарифма равно 10:
H = lgN.

Мера Хартли позволяет решать определенные практические задачи, когда все возможные состояния источника информации имеют одинаковую вероятность.

В общем случае степень неопределенности реализации состояния источника информации зависит не только от числа состояний, но и от вероятностей этих состояний. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния, так как в этом случае результат практически предрешен.

Дата добавления: 2014-01-20