Положение плоскости относительно плоскостей проекций. Линии уровня в плоскости

Линии уровня в плоскости. Линии наибольшего наклона плоскости (линия ската).

Взаимное положение с плоскостью точки и линии. Определение видимости на чертеже.

Следы плоскости.

Положение плоскости относительно плоскостей проекций.

Поверхности. Плоскость. Определение, задание и изображение на чертеже.

1. Поверхности.

Поверхность – это непрерывная совокупность последовательных положений переменной образующей (линии), перемещающейся по определенному закону.

Поверхности могут быть заданы аналитически, то есть уравнениями и называться алгебраическими или трансцендентными, и графически - на чертеже.

Уравнение поверхности Ф (х,у,z) =0 n-ой степени, значит поверхность называется алгебраической n – го порядка. Поверхность первого порядка суть плоскость.

Три точки, не лежащие на одной прямой, определяют положение плоскости в пространстве, поэтому чтобы задать плоскость на чертеже необходимо иметь не менее двух проекций трех точек, не принадлежащих одной прямой (рис.2).

Образование плоскости аналогично образованию комплексного чертежа точки и прямой. Плоскость прямоугольно проецируют на две взаимно перпендикулярные плоскости проекций П1 и П2 (рис.1). Плоскость П1 вращением вниз вокруг оси ох совмещают с плоскостью П2 и получают эпюр двух проекций точек А9,В9,С9 и А0,В0,С0.

С″

А″ А А″ В″ А″ а″

В″

В А′ С′ А′ а′

С″ С′ В′ В′

Рис.2 Рис.3

С′ n″ m ″ k″ l″

Рис.1

m′ n′ k′ l′

Рис. 4 Рис. 5

ЛЕКЦИЯ 3 – 2

В частных случаях плоскость может быть задана, но не ограничена: точкой и не принадлежащей ей прямой (рис. 3); двумя пересекающимися прямыми (рис. 4); двумя параллельными прямыми (рис. 5); плоской фигурой, например, треугольником (рис. 6) и следами (рис.7, 8).

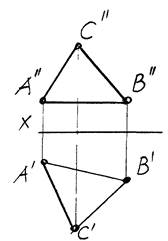
Рис. 6 Рис. 7 Рис. 8

Следом плоскости называется линия пересечения данной плоскости с плоскостью проекций: с горизонтальной плоскостью проекций - горизонтальный след плоскости, с фронтальной плоскостью – фронтальный след плоскости (рис.7, 8).

На рисунках 1,2,3,4,5,6 заданы плоскости общего положения, т.е. не параллельные и не перпендикулярные ни одной из плоскостей проекций.

Плоскости частного положения.

Проецирующие плоскости – перпендикулярные одной из плоскостей проекций. Проецирующая плоскость отображается прямой на плоскость, которой она

перпендикулярна. Эта прямая называется

А″ следом плоскости.

Горизонтально - проецирующая плоскость-

В″ А перпендикулярная горизонтальной плоскости

С″ проекций. Горизонтальная проекция -

В прямая, которая одновременно является

С В′ горизонтальным следом этой плоскости.

А′ На этой линии располагаются горизонталь-

С′ Рис. 9 ные проекции всех точек и линий плоскости.

Лекция 3 - 3

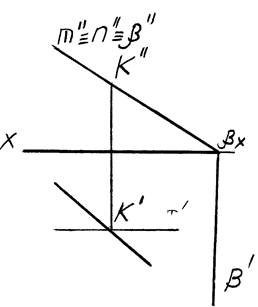
Рис. 10 Рис. 11

Поэтому по фронтальной проекции любого геометрического образа можно построить его горизонтальную проекцию, но обратно горизонтальная проекция точки не определяет ее фронтальную проекцию, т.к. лежит на горизонтально проецирующей прямой. Горизонтально - проецирующая плоскость вполне может быть задана одной своей горизонтальной проекцией. То же относится и к фронтально - проецирующей плоскости.

Фронтально – проецирующая плоскость перпендикулярна фронтальной плоскости проекций. Смотри рис. 11.

Плоскости по отношению к плоскостям проекций могут быть параллельны и тогда они называются плоскостями уровня:

n″ m″

А″ В″ С′ α″ К″′

B′

n′ = m ′= β

A′ C′K′

Рис. 11 Рис. 12

Горизонтальная – плоскость, параллельная горизонтальной плоскости проекций П1

(рис. 11). Фронтальная проекция этой плоскости – линия, параллельная оси проекций ох.

Лекция 3– 4

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций П2 (рис. 12). Горизонтальная проекция этой плоскости - линия, параллельная оси ох.

Профильная – плоскость, параллельная профильной плоскости проекций П3.

Запомните особенности плоскостей частного положения:

Дата добавления: 2014-01-20