Элементарные функции

Следующие функции называются основными элементарными функциями:

1. постоянная
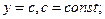
2. степенная
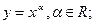
3. показательная
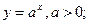
4. логарифмическая
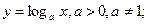
5. тригонометрические
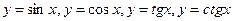
6. обратные тригонометрические .

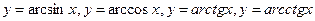Всякая функция f. Которая можетбыть представлена с помощьюформулы 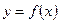,содержащей лишь конечное число арифметических операций надосновными элементарными функциями и композиций, называется элементарной функцией.

В множестве элементарных фуекций выделяются следующие классы функций.

1. Многочлены (полиномы) – функции вида

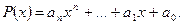
Если 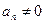, то целое неотрицательное число n называется степенью многочлена Р(х). Функция, тождественно равная нулю, является в силу данного определения многочленом, который называется нулевым многочленом. Степень многочленовобладает тем свойством, чтопри перемножении ненулевых многочленов степень произведения равна сумме степеней сомножителей. Многочлены определены на всей числовой оси.

2. Рациональные функции – функции f(x), представимые в виде

,

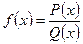где P(x) и Q(x) многочлены (Q(x) – ненулевой многочлен). Функция f(x) определена во всех точках числовой оси, кроме тех ее точек, где знаменатель Q(x) обращается в ноль.

3. Иррациональные функции, т.е. такие функции, не являющиеся рациональными, которые могут быть заданы композицией конечного числа рациональных функций, степенных функций с рациональными показателями и четырех арифметических действий.

4. Трансцендентальные функции – элементарные функции, не являющиеся рациональными или иррациональными.

Дата добавления: 2014-01-20