Статическая оптимизация

К статической оптимизации относят задачи определения экстремума функции цели в зависимости от значений переменных параметров системы и управляющих воздействий, не являющихся функцией времени. Одна из наиболее распространенных задач – нахождение экстремума того или иного ТЭП. Задача статической оптимизации для промышленных установок также, как правило, является условной.

Рассмотрим задачу статической оптимизации на следующем примере. Имеется котельная, в которой установлены пять котлов. Данные пять котлов должны выдавать заданное количество тепла , при этом на количество тепла, выдаваемого каждым котлов, накладываются ограничения сверху и снизу. Необходимо минимизировать суммарный расход топлива на котельную при соблюдении указанных ограничений.

Математически постановка задачи будет выглядеть следующим образом.

Целевая функция:

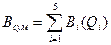(5.4)

Ограничения:

(5.5)

(5.6)

Существуют различные методы решения задач статической оптимизации – прямой метод, метод неопределенных множителей Лагранжа, метод динамического программирования, симплекс-метод (метод деформируемого многогранника) и т.д. Все они имеют свои достоинства и недостатки и свою сферу применения. Остановимся более подробно на одном из них – методе Гаусса-Зайделя.

Метод Гаусса-Зайделя (метод покоординатного спуска)

Данный метод рассмотрим на примере задачи оптимизации для целевой функции, зависящей от двух переменных – х1 и х2. Для определенности положим, что целевую функцию нужно максимизировать. На независимые переменные сверху и снизу накладываются ограничения. Математическая постановка данной задачи будет выглядеть следующим образом:

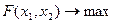(5.7)

(5.8)

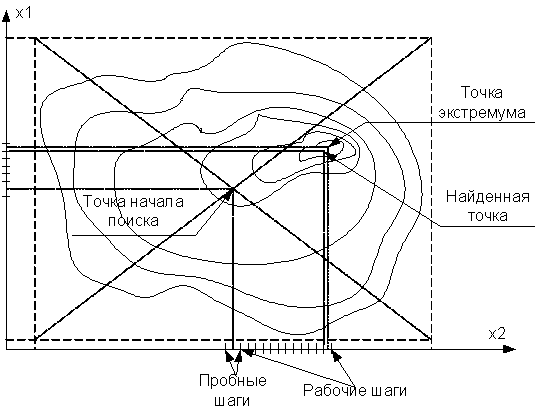
Иллюстрация к методу Гаусса-Зайделя представлена на рис. 5.1.

Рис. 5.1.

Сначала необходимо внутри допустимой области выбрать точку начала поиска, обычно она выбирается в центре области, если нет оснований выбрать ее в другом месте. Далее одна из переменных фиксируется, вторую варьируют – делают пробные шаги с целью определения направления движения. По результатам каждого шага рассчитывают значение целевой функции. Направлением движения в данном случае будет направление возрастания целевой функции. В этом направлении делаются рабочие шаги вдоль соответствующей оси координат до тех пор, пока на очередном шаге ЦФ не начнет уменьшаться. Тогда возвращаются на шаг назад, текущую варьируемую переменную фиксируют и делают все описанные шаги по другой переменной.

Точность нахождения экстремума зависит величины шага. При этом необходимо учитывать, что при чрезмерном уменьшении шага увеличивается время поиска.

Несомненным достоинством данного метода является его простота. Основной недостаток – долгое время поиска экстремума.

Дата добавления: 2014-01-20