Тема: Оценка параметров генеральной совокупности

.

Напомним, что закон больших чисел говорит о том, что действие большого числа случайных факторов приводит к результату, который перестает быть случайным. В нашем случае, чем больше объем выборки, тем маловероятное ошибки при оценивании. Тогда, если оценка состоятельна, то практически достоверно, что при достаточно большом n 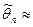q.

Опр. Несмещенная статистическая оценка называется эффективной, если она при одних и тех же объемах выборки имеет наименьшую дисперсия.

Эффективность оценки 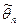определяют отношением:

,

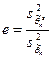где соответственно дисперсии эффективной и данной оценок. Чем ближе е к 1, тем эффективнее оценка.

В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности.

Теорема 1: выборочная доля 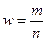повторной выборки есть несмещенная и состоятельная оценка генеральной доли 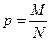, причем дисперсия

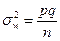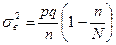, ()где .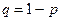

Теорема 2: выборочная средняя 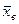повторной и бесповторной выборки есть несмещенная и состоятельная оценка генеральной средней 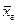, причем ее дисперсия

().

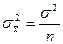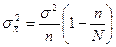Теорема 3. Выборочная дисперсия s² повторной и бесповторной выборок есть смещенная и состоятельная оценка генеральной дисперсии.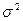

Выборочная дисперсия занижает генеральную дисперсию.Поэтому, заменяя 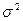на s², мы допускаем систематическую погрешность в меньшую сторону. Чтобы ее ликвидировать, достаточно ввести поправку, умножив s²- на 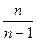. Тогда с учетом получим «исправленную» выборочную дисперсию

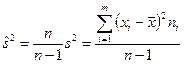
Т.е. 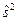является несмещенной и состоятельной оценкой генеральной дисперсии .

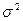Дисперсию «исправляют» в случае, когда объем выборки меньше 30 вариантов.

Пример. Найти несмещенную оценку средней и дисперсии случайной величины Х на основании данного распределения выборки

xi					∑
ni

Решение:

Составим расчетную таблицу

хi	ni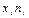
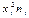
			76,197
			12,3709
			6,848
			26,721
Сумма			122,138

Найдем среднюю выборочную:

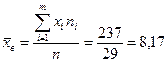
По теореме 2 средняя выборочная является несмещенной и состоятельной оценкой генеральной средней, поэтому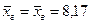

Найдем выборочную дисперсию:

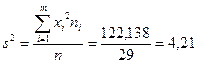
Дисперсия при n < 30 в силу теоремы 3 является смещенной и состоятельной оценкой генеральной дисперсии, поэтому ее необходимо «исправить»:

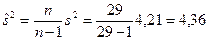
Теперь дисперсия является несмещенной и состоятельной оценкой генеральной дисперсии.

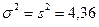
Дата добавления: 2014-01-20