
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторное произведение
|
|
|
|
Упорядоченная тройка некомпланарных векторов 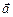 ,
,  ,
,  называется правой тройкой, если наблюдателю, находящемуся в конечной точке вектора
называется правой тройкой, если наблюдателю, находящемуся в конечной точке вектора  , поворот от вектора
, поворот от вектора 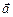 к вектору
к вектору  на кратчайший угол виден совершающимся против часовой стрелки.
на кратчайший угол виден совершающимся против часовой стрелки.
Если поворот от вектора 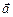 к вектору
к вектору  на кратчайший угол виден совершающимся по часовой стрелке, то векторы
на кратчайший угол виден совершающимся по часовой стрелке, то векторы 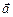 ,
,  ,
,  образуют левую тройку.
образуют левую тройку.
 |
правая тройка левая тройка
Векторным произведением двух векторов 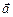 и
и  , обозначаемым
, обозначаемым 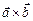 , называется вектор, удовлетворяющий следующим условиям:
, называется вектор, удовлетворяющий следующим условиям:
1) длина (модуль) векторного произведения равна  , где
, где 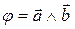 . Т.е. модуль векторного произведения равен площади параллелограмма, построенного на этих векторах;
. Т.е. модуль векторного произведения равен площади параллелограмма, построенного на этих векторах;
2) вектор 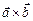 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 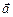 и
и  :
: 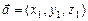 ,
, 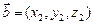
3) векторы 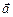 ,
,  ,
,  образуют правую тройку.
образуют правую тройку.
Из определения ясно, что  , если один из них нулевой или они коллинеарны (
, если один из них нулевой или они коллинеарны ( ).
).
Справедливы следующие свойства векторного произведения:
1)  ;
;
2) векторное произведение антикоммутативно: 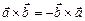 ;
;
3)  , где
, где  ‑ число (скаляр);
‑ число (скаляр);
4) векторное произведение дистрибутивно относительно сложения векторов:  .
.
Зная координаты векторов 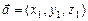 и
и 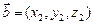 в декартовой прямоугольной системе координат, для вычисления векторного произведения векторов
в декартовой прямоугольной системе координат, для вычисления векторного произведения векторов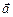 и
и  можно воспользоваться следующей формулой:
можно воспользоваться следующей формулой:
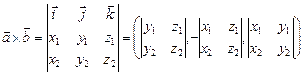 (определитель разложен по первой строке).
(определитель разложен по первой строке).
Смешанным произведением векторов 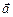 ,
,  ,
,  называется число
называется число  , которое равно скалярному произведению векторного произведения
, которое равно скалярному произведению векторного произведения 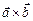 и вектора
и вектора  :
:  .
.
 |
Основные свойства смешанного произведения векторов:
1)  , т.е. порядок двух операций (скалярное и векторное произведение векторов), дающих смешанное произведение векторов, не является существенным. Это свойство и позволяет обозначать смешанное произведение просто
, т.е. порядок двух операций (скалярное и векторное произведение векторов), дающих смешанное произведение векторов, не является существенным. Это свойство и позволяет обозначать смешанное произведение просто  ;
;
2)  , т.е. при нарушении цикличности перестановки векторов знак векторного произведения меняется на противоположный;
, т.е. при нарушении цикличности перестановки векторов знак векторного произведения меняется на противоположный;
3)  , где
, где 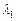 и
и 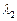 - числа (скаляры).
- числа (скаляры).
Зная координаты векторов 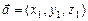 ,
, 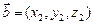 и
и  в декартовой прямоугольной системе координат, для вычисления смешанного произведения векторов
в декартовой прямоугольной системе координат, для вычисления смешанного произведения векторов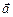 ,
,  и
и  можно воспользоваться следующей формулой:
можно воспользоваться следующей формулой:
 =
=
Условие компланарности векторов: Смешанное произведение равно нулю тогда и только тогда, когда векторы 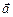 ,
,  ,
,  компланарны.
компланарны.
В самом.деле, равенство  означает, что векторы
означает, что векторы 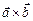 и
и  перпендикулярны. Но
перпендикулярны. Но 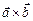 есть вектор, перпендикулярный и
есть вектор, перпендикулярный и 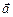 и
и  . Стало быть,
. Стало быть, 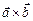 перпендикулярен всем трем векторам одновременно. Это возможно лишь в случае, когда они лежат в одной плоскости;
перпендикулярен всем трем векторам одновременно. Это возможно лишь в случае, когда они лежат в одной плоскости;
Геометрический смысл смешанного произведения:
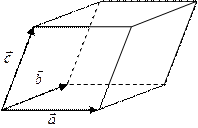 Смешанное произведение равно объему параллелепипеда, построенного на векторах
Смешанное произведение равно объему параллелепипеда, построенного на векторах 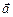 ,
,  ,
,  и взятого со знаком «+», если тройка правая, и со знаком «—», если тройка левая:
и взятого со знаком «+», если тройка правая, и со знаком «—», если тройка левая: 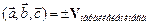 .
.
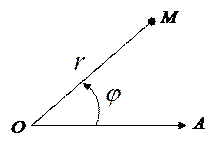 Воспользовавшись геометрическим смыслом смешанного произведения векторов, можно определить тип тройки векторов по знаку смешанного произведения векторов. Если
Воспользовавшись геометрическим смыслом смешанного произведения векторов, можно определить тип тройки векторов по знаку смешанного произведения векторов. Если  , то
, то 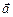 ,
,  ,
,  ‑ правая тройка векторов, если
‑ правая тройка векторов, если 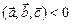 , то
, то 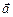 ,
,  ,
,  ‑ левая тройка векторов.
‑ левая тройка векторов.
Полярная система координат.
| Говорят, что на плоскости введена полярная система координат, если заданы: 1) т.О (полюс); 2) полупрямая ОА (полярная ось); 3) масштаб для измерения длин. |
Положение произвольной точки М на плоскости определяется полярными координатами: полярным радиусом  (
(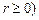 и полярным углом
и полярным углом 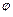 между полупрямыми
между полупрямыми 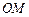 и
и  . Считают, что
. Считают, что  при повороте от
при повороте от  к
к 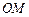 против часовой стрелки и
против часовой стрелки и  при повороте от
при повороте от  к
к 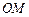 по часовой стрелке. Полярный угол определен не однозначно – значение полярного угла, удовлетворяющее условию
по часовой стрелке. Полярный угол определен не однозначно – значение полярного угла, удовлетворяющее условию 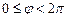 , называется главным.
, называется главным.
 Определим связь между декартовыми координатами на плоскости и полярными координатами. Для этого совместим начало координат и полюс, а полярную ось направим по положительной полуоси абсцисс. Тогда декартовы координаты
Определим связь между декартовыми координатами на плоскости и полярными координатами. Для этого совместим начало координат и полюс, а полярную ось направим по положительной полуоси абсцисс. Тогда декартовы координаты  и полярные координаты
и полярные координаты 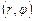 произвольной точки М связаны следующими соотношениями:
произвольной точки М связаны следующими соотношениями:
 и и 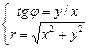 . .
|
При нахождении полярного угла необходимо учитывать, в какой координатной четверти расположена т. М и подобрать соответствующее значение  .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1403; Нарушение авторских прав?; Мы поможем в написании вашей работы!